Эти уравнения определяют процесс преобразования точки а на положительной полуоси х в точку с на этой же полуоси. Если c<z а, траектории будут скручиваться и генератор будет совершать затухающие колебания. Если с> а, траектории раскручиваются и колебания нарастают. Если с = Ь, колебания становятся незатухающими и траектория превращается в замкнутый цикл (рис. 7.20, б). Уравнения (7.17), называемые уравнениями точечного преобразования, позволяют найти параметры цикла. Положив а = с, решим уравнения (7.17) относительно а и Ъ:

а = / /(1 - V): = Y (l Y)- (7.18)

Если у ф \, решение единственно и, следовательно, любая другая точка в окрестности а уже не принадлежит замкнутому циклу. Таким образом, найденный замкнутый цикл является изолированным. Изолированную замкнутую траекторию называют предельным циклом. Предельный цикл окружен навивающимися на него или скручивающимися с него траекториями. Если в результате малого смещения с цикла в любом направлении мы попадаем на траекторию, неограниченно приближающуюся к циклу, то цикл устойчив. Устойчивый предельный цикл соответствует устойчивым колебаниям, называемым самовозбуждающимися или ав-токолебаниями. Отклонение параметров автоколебаний (амплитуды, частоты и т. п.) малой помехой в процессе дальнейшего движения уменьшается - этим автоколебания принципиально отличаются от незатухающих колебаний в линейных системах. Линейные генераторы не применяются, так как они не обеспечивают устойчивого колебательного движения.

Пусть между сна существует зависимость

с-Т{а), (7.19)

где Т (а) - функция последования.

Если в результате возмущения точка сместится с цикла, то по истечении периода получим приращения Аа и Дс, связанные зависимостью lim (Дс/Да) = dTlda.

Если dTlda <Z 1, то Дс <; Да, начальное отклонение уменьшается и предельный цикл устойчив, в противном случае - неустойчив. В рассмотренном примере

c = v« + (l+T)/; дTдa=y = e-<<l,

поэтому предельный цикл устойчив.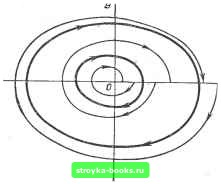

Рнс. 7.21

Фазовый портрет системы представлен на рис. 7.20, б. В начале координат имеем неустойчивый фокус. Где бы внутри предельного цикла ни находилась изображающая точка, с течением времени она будет приближаться к циклу. В такой системе автоколебания возникают «сами собой», от сколь угодно малого возмущен и я. Возбуждение колебаний такого рода

называют мягким. На рис. 7.21 представлен фазовый портрет с двумя предельными циклами: внутренним неустойчивым и внешним устойчивым. Начало координат - устойчивый фокус. Движение, возникнув внутри внутреннего цикла, с течением времени прекратится и автоколебания не возникнут. Чтобы их возбудить, необходим достаточно сильный толчок, выводящий начальную точку за предельный неустойчивый цикл. Это система с жестким возбуждением автоколебаний. Примерами таких систем являются стенные гиревые часы с маятником или плохо налаженный микрофон в аудитории, когда резкое усиление голоса оратора приводит к микрофонному эффекту. Неустойчивый предельный цикл соответствует наличию формального периодического решения уравнений, но не физически существующим автоколебаниям. Он ограничивает в фазовой плоскости область допустимых начальных возмущений, при которых состояние равновесия еще остается устойчивым.

§ 7.4, Системы с переменной структурой

К системам с переменной структурой (СПС) относят системы, структурная схема которых изменяется при переходе изображающей точки через границы некоторых заранее установленных областей фазового пространства. Примерами систем с переменной структурой являются релейные системы, замыкающие или размыкающие часть схемы при переходе через ли-

J-*. 1/s -A- 5

НЙИ переключения. В систе-/5 мах с переменной структурой возможно при определенных условиях получать виды движения - более высокого Karl чества, чем в любой из отдельно взятых структур, образующих СПС. Один из способов построения СПС состоит в «сшивании» желаемым образом отдельных областей фазового пространства. Так, в ,22 рассмотренной выше системе с сухим постоянным трением благодаря смещению фазовых полуплоскостей замкнутые траектории превратились в траектории, скручивающиеся к отрезку покоя. Еще более быстрое затухание при схождении траекторий уже не к отрезку покоя, а к началу координат, т. е. при более высокой точности управления, имело место в системе с переменным сухим трением. Упомянутые две системы можно рассматривать как системы с переменной структурой, в которых переход от одной структуры к другой обусловлен внутренними физическими законами, действующими в данной системе. Любая из них может быть воспроизведена искусственно путем введения в систему переключающих логических элементов. На рис. 7.22 показана СПС - аналог системы с переменным сухим трением. Схема состоит из двух интегрирующих элементов, усилителей с коэффициентами усиления woi и соог и двухпозиционного поляризованного реле Р, питаемого от блока произведения П. Реле реагирует на знак произведения xdxidt = хуи осуществляет переключение цепи обратной связи по закону

«01, ху>0; • . • ; .

«>02, ху<:о, ,

причем юо1 > 002- Уравнения системы

x-fc)gix = 0; sign х = signх;

х + <йх=0; sign х = -sign X ; .!

и условия переключения х«/ = О подобны <7.10). "

Другой способ состоит в получении вырожденных движений по совокупности устойчивых фазовых траекторий. Если для йё-