
 |
|
Главная Нелинейные системы управления [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [ 71 ] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] V(t) 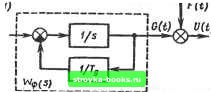 <2b- с it) /А f 1/Ts \X(t) \ yjonrJSl V(t)\
Рис. 9.21 Подставляя в (9.152) t-*- со, находим выражение для дисперсии ошибки в установившемся режиме: N 0.5p(l + Vl4-p) <е 1+0.5Р + У1+Р Vi + p+i 6. В соответствии с (9.145) находим функцию С {t): r(t) 1 С(/) = - 0,5р(1 -Vl+p)-0.5(l+Vl+p)eP* (1+0,5р-УТ+р)-(1 + 0,5р + l/T+p) еР (9.153) Из (9.153) находим начальное значение коэффициента С (0) (при t=h = 0). т. е. C(0) = p/27g = Dg/N. в значение коэффициента С (оо) в установившемся режиме (прн / т. е. С(оо) = р/[Гв(1 + УТТр)1- 7. Дифференциальное уравнение оптимального фильтра Калмана-Бьюси в соответствии с (9.147) имеет вид dX {fjidt = -X (t)/Tg + C(t)[U {f) - X (0I< Структурная схема, соответствующая этому дифференциальному уравнению, приведена на рис. 9.21, б. Заменяя интегрирующее звено, охваченное обратной связью, инерционным звеном, можно представить структурную схему так, как показано на рис. 9.21, в. Используя эту структурную схему и значения передаточных функций отдельных ее динамических звеньев, определяем для установившегося режима передаточную функцию замкнутой оптимальной системы: йз.опт (S) = [С (оо) Tgl{ 1 + sTg)y[\ + С (оо) 7g/( 1 + sTg)\ =KI(\-\-Ts), где C{co)Tg p 1 . l + C{co)Tg ,+p/(i + yi+p) yr+7 Полученное выражение для передаточной функции оптимального фильтра Калмана-Бьюси полностью совпадают с выражением для передаточной функции фильтра Винера, найденного в примерах 9.6 и 9.7. Следует обратить внимание на то, что даже при стационарных случайных воздействиях в переходном режиме оптимальный фильтр Калмана-Бьюси является нестационарным, поскольку коэффициент C{t) изменяется во времени. § 9.8. Случайные процессы в линейных импульсных системах Аналогом непрерывной реализации случайного процесса Х(7) для импульсных систем является дискретная (решетчатая) реализация Xi {п\ (рис. 9.22, а), представляющая собой последовательность ординат, совпадающих с соответствующим значением непрерывной реализации Xi{t) в дискретные моменты относительного времени t = tiT = п, где Т - период квантования. Совокупность решетчатых реализаций Xi Ы] называют диек-ретным {решетчатым) случайным процессом Х\п\. Дискретные случайные процессы, по аналогии с непрерывными случай- 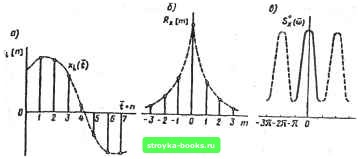 я гл ля гз Рис. 9.22 ными процессами, могут характеризоваться такими статистическими характеристиками, как математическое ожидание (момент первого порядка), корреляционная функция (момент второго порядка) и т. д. Математическое ожидание и корреляционная функция (а также любые моменты т-го порядка) дискретного случайного процесса равны математическому ожиданию и корреляционной функции (моменту т-го порядка) соответствующего непрерывного случайного процесса, взятым в дискретные моменты времени t = п. В дальнейшем будем рассматривать стационарные эрго-дические случайные процессы. В этом случае среднее значение по множеству (математическое ожидание) равно среднему значению по времени, которое определяется следующей суммой: т = X [п] = lim (9.154) Где х[п\ - любая реализация дискретного случайного процесса. Среднее значение квадрата стационарного случайного процесса (с равным нулю средним значением) называют дисперсией дискретного случайного процесса: (9.155) [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [ 71 ] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] 0.0013 |