сигнала уменьшается и при очень большом уровне помех оказывается близким к нулю.

Таким образом, увеличение уровня помех, определяемого дисперсией случайного входного сигнала, уменьшает полезный сигнал на выходе нелинейного элемента, что эквивалентно уменьшению коэффициента преобразования нелинейного элемента.

Одновременно с этим выходной сигнал обогащается как высокочастотными, так и низкочастотными гармониками, т. е. происходит изменение спектрального состава выходного случайного процесса по сравнению со спектральным составом входного случайного процесса.

Допустим, например, что на нелинейный элемент типа насыщения поступает случайный сигнал, среднее значение которого mj,, а плотность вероятности w{y) соответствует нормальному закону распределения (рис. 9.24).

Линейный участок характеристики в пределах ±t> ие оказывает влияния на форму кривой плотности вероятности, т. е. ш(х) = w{y) при \у\ < Ь.

Выходной сигнал нелинейного элемента не может превышать уровня насыщения В, поэтому вероятность появления сигнала, большего по абсолютной величине, чем Б, равна нулю, т. е. ш(х) = О- при у > Ь.

Всем значениям входного сигнала у > b нлк у <: -Ь будет соответствовать значение выходного сигнала х = В или х = -В. поэтому вероятность получения величины В или -В на выходе нелинейного элемента сильно возрастает и становится равной величине заштрихованной площади под участком кривой плотности вероятности входного сигнала, лежащей в пределах от у = Ь до у = со. Это выразится в том, что плотность вероятности выходного сигнала w(x) в точках у = ±Ь будет представлять собой 6-функции, т. е. им- SVz-s, пульсы бесконечно большой величины и бесконечно малой ширины, площадь S которых равна заштрихованной площади под соответствующим (правым или левым) участком кривой плотности вероятности входного сигнала.

Таким образом, выражение для плотности вероятности выходного сигнала можно записать так:

W {у) при \у\<:Ь;

t«()= 6(i,q: Ь) прн = (9.168)

О при I у I > Ь.

Общая площадь под кривой плотности вероятности выходного

сигнала, естественно, остается равной единице, т. е. J ш (x)rfco =

- 1. - ; л • . ~-

Исследование нелинейных систем, находящихся под воздействием случайных процессов, значительно сложнее, чем линейных систем.

Общих точных методов исследования подобных систем нет, и для изучения систем в этом случае обычно используют приближенные методы.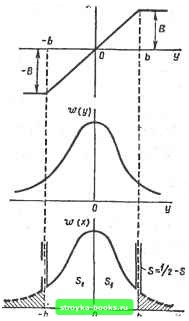

Рис. 9.24

§ 9.10. Статистическая линеаризация нелинейных элементов

Наибольшее распространение в практике расчета нелинейных систем при случайных воздействиях получил приближенный метод, называемый методом статистической линеаризации, разработанный в 1954 г. одновременно И. Е. Казаковым в СССР и Р. Бутоном в США.

Идея метода основана на приближенной замене нелинейных преобразований процессов, происходящих в системе, статистически эквивалентными им линейными преобразованиями, при этом нелинейный элемент заменяется статистически эквивалентным линейным элементом. В результате такой замены система в целом линеаризуется и для ее исследования можно применять аппарат линейной теории.

Возможны различные критерии статистической эквивалентности, которые могут быть положены в основу метода статистической линеаризации. В тех случаях, когда линеаризуют безынерционный нелинейный элемент, у которого нелинейная зависимость между входным y{t) и выходным x{f) сигналами имеет вид

x{t) [y{t)], (9.169)

где ф - статическая характеристика нелинейного элемента, применяют следующие два критерия:

1. Критерий равенства математического ожидания и дисперсии случайного процесса на выходе нелинейного элемента и эквивалентного ему линейного элемента.

2. Критерий минимума математического ожидания квадрата разности случайных процессов иа выходе нелинейного элемента и эквивалентного ему линейного элемента.

Познакомимся с этими критериями, ограничиваясь рассмотрением только однозначных нелинейных характеристик, которые могут быть либо нечетными, либо четными.

Напомним, что для нечетных и четных характеристик соответственно справедливы соотношения

ф(-г/) =-ф(.у); (9-170)

ф(-у) ¥.У)- (9-171)