Случайные процессы на входе и выходе нелинейного элемента могут быть представлены следующим образом:

У(/) = т,(0 + К(0; (9.172)

X(t)=mAt)-h°X (t). (9.173)

где my(t), tnx{t) - математические ожидания входного и выходного сигналов соответственно, включающие медленно меняющиеся регулярные составляющие; Y{t), X{t) - центрированные случайные составляющие процессов на входе и выходе нелинейного эле?к{еита соответственно.

Заметим, что для четных нелинейных характеристик, обладающих выпрямляющими свойствами, математическое ожидание /Лзс(0 отлично от нуля даже при /п„(/) = 0.

В общем случае для однозначной нелинейной функции 4>iy) произвольного вида сигнал на выходе эквивалентного линеаризованного элемента

и (/) = Фо [ту) + kl Y (О =-т„ (О + Ь (t). (9.174)

где Фо {гПу) - математическое ожида1П1е нелинейной функции фО/). fi - эквивалентный статистическнй коэффициент усиления по случайной центрированной составляющей.

Таким образом, в общем случае нелинейный безынерционный элемент (рис. 9.25, а) заменяют двумя безынерционными элементами: нелинейным по математическому ожиданию и линейным по случайной центрированной составляющей (рис. 9.25. б).

В частном случае, когда нелинейный безынерционный элемент имеет нечетную характеристику, функция фо может быть представлена в виде

Ф„ = /го/п,(0, (9.175)

где k„ - эквивалентный статистический коэффициент усиления нелинейного элемента по математическому ожиданию (гю средней составляющей).

В этом случае нелинейный элемент можно эквивалентно заменить двумя линейными элементами с коэффициентами усиления kg и kl (рис. 9.26). Числовые значения этих коэффициентов при заданной нелинейной зависимости ф определяются значениями математического ожидания п дисперсии случайного сигнала иа входе нелинейного элемопта.

Покажем сначала, как находят коэ1}х{)цциенты ф, k, ki в случае статистической линеаризации, основанной на первом

EW-X(t)-UH)

my(t) I

nt) 1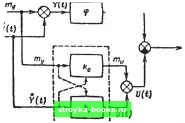

Рис. 9.25

Рис. 9.26

критерии статистической эквивалентности, состоящем в выполнении равенства математического ожидания и дисперсии случайного процесса на выходе нелинейного элемента и эквивалентного ему линейного элемента, т. е. когда

/".(OHuW; (9.176)

DAf)-DAt)- (9.177)

Принимая во внимание (9.174), получаем

Фо=/пЛО=/пЛО- (9.178)

Для нечетных нелинейностей, учитывая (9.175), получим

/г„=тЛО/т«(0. (9.179)

Чтобы найти статистически эквивалентный коэффициент ку, перепишем (9.177) следующим образом:

Dx (О = it) M\{U {т М l{k, Y т + k\ Dy it),

откуда

Л. = АГ = К Dx {l)/Dy (О = ±ах (D/Oy (О- (9.180)

Обозначение /г" показывает, что коэффициент /г, найден по первому критерию эквивалентности.

Статистические коэффициенты фо, kg и ftj можно также выразить через нелинейную зависимость ф и плотность вероятности w{y) случайного сигнала К(/) на входе нелинейного элемента:

(9.181)

0 = =-- f 4>{y)w{y)dy; (9.182) my(t) my(t) J

j 4>4y)w{y)dy -ml(t)

VDy(t)

. 9.183)

Знаки в (9.180) и (9.183) следует выбирать такими, чтобы знаки X(t) и U{f) совпадали.

Второй критерий статистической эквивалентности требует выполнения условия минимума математического ожидания квадрата разности процессов на выходе нелинейного элемента и эквивалентного линейного элемента, т. е.

=ГМ [{X (О- и (t)Y] = min. (9.184)

Подставляя в (9.184) значения X (t) и U{t), определяемые по (9.173) и (9.174), получим

М [{т, (t) + X(О-Фо ~k,Y т = min.

После выполнения операции возведения в квадрат и вычисления математического ожидания имеем

- 2ф„т(0-2ftii?« (0)=:min, (9.185)

где m{i) - математическое ожидание случайного процесса на выходе нелинейного элемента; Dy{t) = Ml{Y{t)}, DJt) = = М[{ХЩ)У\ - дисперсия центрированного случайного процесса на входе и выходе нелинейного элемента соответственно; х°у (0) = DOy (f) = MIX (О Y (f)] - математическое ожидание (среднее значение) произведения двух случайных функций X(rf) и Y{t), равное начальному значению взаимной корреляционной функции R°y(0).

?=«При заданных значениях т (t), Dy (t), D{t), R°y{0)

величина является функцией параметров фо и ki.

Значения фо и k, при которых выполняется (9.184), найдем, если приравняем нулю частньге производные функции

по параметрам ф„ и k. Имеем dfldg = 2ф„ - 2т {t) = = О, откуда

Фо = т,(0. (9.186)