
 |
|
Главная Нелинейные системы управления [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [ 79 ] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166]
E(t) X(t) U(t) Рис. 9.30 случае на основе метода статистической линеари- гпд зации сигнал на выходе "~* нелинейного элемента приближенно может быть записан следующим о образом: /1 + kl (me, D,) Ё (0, (9.211) где m„ - математическое ожидание сигнала на выходе нелинейного элемента; t/(0 - центрированная составляющая случайного процесса на выходе нелинейного элемента; koinie, D е) - эквивалентный статистический коэффициент усиления нелинейного элемента по математическому ожиданию; fci (т, De)-эквивалентный статистический коэффициент усиления нелинейного элемента по случайной составляющей. В результате статистической линеаризации нелинейный элемент эквивалентно заменяется двумя линейными безынерционными элементами: один из них с коэффициентом усиления ко и второй - с коэффициентом усиления й. При этом исходная нелинейная замкнутая система (рис. 9.29) эквивалентно заменяется двумя замкнутыми связанными линеаризованными системами (рис. 9.30): по математическому ожиданию; по центрированной случайной составляющей. Передаточные функции разомкнутых линеаризованных систем равны: по математическому ожиданию W„e(s) = ko{m, D)W{s), по центрированной случайной составляющей W7c(s)=fei(me, Ds)W(s). (9.212) (9.213) Передаточные функции замкнутых линеаризованных систем относительно ошибки равны; по математическому ожиданию Trig me (S)- : (9.214) по центрированной случайной составляющей 1 I W " . (s) = - 1 (s) (9.215) Передаточные функции (9.212) и (9.213) взаимосвязаны через коэффициенты и Л,, которые являются функциями неизвестных величин т н D . Заметим, что полученные таким образом две связанные ли-иеаризованные системы будут линейными только при определенных постоянных значениях и D, т. е. при стационарном режиме системы. При нестационарном режиме система остается нелинейной, так как коэффициенты feo н fej, зависящие от и .D £, будут переменными. Если случайный процесс G{i) на входе системы стационарный, то = const. В этом случае математическое ожидание ошибки связано с математическим ожиданием rig входного сигнала следующим соотношением: т,. (9.216) Дисперс1[Я ошибки оо оо = f 5 = (со) do> = j" \ W. (;о>) f 5j (со) dco. (9.21 7) - со - оо где 5 (со) - спектральная плотность центрированной случайной составляющей C{f) входного сигнала; 5° (со) = 1 X X (/со) р 5 °g (со) - спектральная плотность центрированной случайной составляющей ошибки. Уравнения (9.216) и (9.217) образуют систему алгебраических уравнений: 2п J (9.218) Система уравнений (9.218) содержит два неизвестных и De и коэффициенты feo и fei. яв.аяющнеся функциями этих неизвестных. Решая снг-ем\ уравнений, можно найти мате- 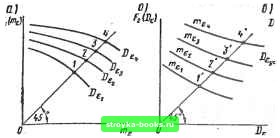 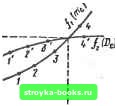 Рис. 9.31 магическое ожидание тк дисперсию D ошибки в установившемся режиме. Решение системы уравнений (9.218) можио произвести либо методом последовательных приближений, либо графоаналитическим методом. При решении методом последовательных приближений задаются вначале некоторыми значениями коэффициентов kg иfti и по(9.216) и (9.217) находят /Пе и в первом приближении. По найденным значениям тмО уточняют величины kg и fti. пользуясь (9.193), (9.194). (9.195), (9.190) нли графиками зависимостей kg (m. D„), k (my, Dy), приведенными в приложении 9.2. Затем весь цикл вычислений коэффициентов kg и fti повторяется многократно до тех пор, пока в процессе приближений последующие значения коэффициентов не будет с достаточной точностью совпадать с предыдущими значениями. Решение графоаналитическим методом производится обычно тогда, когда уравнения системы (9.218) имеют сложный вид. В этом случае в координатах т-О строят кривые, соответствующие обоим уравнениям системы (9.218); точка пересечения этих кривых дает решение указанной системы уравнений. Графоаналитическое решение уравнений (9.218) целесообразно проводить в такой последовательности: 1. Строят семейство функций = Fi{m) (рис. 9.31, а), ирпрльзуя первое уравнение системы (9.218) для различных фиксированных значений D const 2. Проводят прямую из начала координат под углом 45° и по точкам пересечения ее с кривыми семейства F строят график D fi(m (рис. 9.31. е), 3. Строят семейство функций F = F (D ) (рис. 9.31, б), используя второе уравнение системы (9.218) для различных фиксированных значений mi = const. [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [ 79 ] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] 0.0013 |