
 |
|
Главная Нелинейные системы управления [0] [1] [2] [3] [4] [5] [6] [ 7 ] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] которой линейной подструктуры СПС существует хотя бы один действительный отрицательный корень характеристического уравнения, то существует и соответствующая этому корню совокупность устойчивых движений, занимающая в фазовом пространстве некоторое подпространство. Пусть характеристическое уравнение имеет m левых я п - IL- т правых корней. Тогда решение однородного уравнения таково: т , п «"=1 i=m+l где В] - произвольные постоянные, соответствующие правым корням. Выбирая соответствующим образом начальные условия, всегда можно обратить в нуль любую из произвольных постоянных. Выберем их так, чтобы все Bj обратились в нуль. Тогда оставшиеся члены образуют совокупность устойчивых движений: л:= 2 • (7-20) Если за фазовые координаты приняты л: и ее производные до п - 1 включительно, то первые т координат х, х, х"~, удовлетворяющие (7.20), будут линейно зависимыми и образуют подпространство, попав в которое изображающая точка будет двигаться в нем к состоянию равновесия. Можно далее обратить в нуль и некоторые С,, тогда порядок подпространства понижается. Если обращены в нуль все С, кроме одной то подпространство вырождается в линию, проходящую через начало координат.Такая прямая имеется на рис. 7.12 и 7.16 и. соответствует частному решению с отрицательным действительным корнем. Если оставить отличными рт нуля две постоянные С, и Cg, соответствующие либо паре действительных, либо паре сопряженных комплексных левых корней, то подпространство вырождается в плоскость, вид траекторий в которой соответствует рис. 7.16 при действительных и рис. 7.15 при комплексных корнях. Подбирая соответствующим образом законы переключения, можно обеспечить обяза-Т)льное попадание. изображающей точки в подпространство Рис. 7.23 устойчивых движений. Проиллюстрируем это на простом примере (рис. 7.23). Уравнения системы dxIdt == у; dyldt = + alx. Фазовые траектории для верхнего и нижнего знаков показаны соответственно на рис. 7.12 и 7.8. Выбираем в качестве линий переключения линию у = - сооХ (устройчнвую асимптоту) и ось ординат х = 0. Поляризованное реле реагирует на величину {х, г/) = - соо sign \{у -f ы)х]. Движение показано на рис. 7.24. Если оно началось в точке Л о, то идет сначала по неустойчивой гиперболической фазовой траектории, затем по пересечении оси у переходит на эллиптическую, и попав на линию Afi-подпространство вырожденных устойчивых движений, проходит по ней до точки равновесия. Небольшие промахи при переключении, смещающие изображающую точку с прямой (точка Л g), не нарушают устойчивости. Более сложные примеры рассматриваются в специальной литературе. Весьма интересные свойства имеют СПС, в которых вырожденные движения создаются по искусственным линиям, получаемым с помощью подбора законов пере-р„с. 7.24 ключения подпрост- 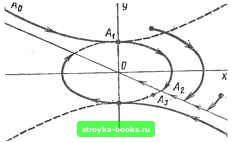 Рис. 7.25 панств, не являющихся совокупностью фазовых траекторий системы. Частным случаем такой СПС является релейная система с линейной частью в виде двух интеграторов. На рис. 7.25 показана простейшая релейная система. Ее линейная часть, состоит из двух включенных последовательно идеальных интеграторов, нелинейным элементом (НЭ) является реле. Если реле заменить линейным усилителем с характеристикой z = Ф {х)= = kx, замкнутая система будет линейной консервативной с фазовым портретом в виде семейства концентрических эллипсов. Уравнения релейной системы dx/dt = у; dyldt = - Ф (х). (7.21) Уравнение фазовой траектории dyldx = - Ф (х) t/. В случае идеального реле с характеристикой 7 (см. рис. 7.6) k, х>0, Z =Ф (х) = -k, х<0. Тогда из (7.21) получим dyldx = ± kly или уЧ2 ± kx= С. (7.22) Верхний знак соответствует правой, нижний - левой полуплоскости. Ось ординат является линией переключения. Фазовые траектории - замкнутые кривые, образованные отрезками парабол (рис. 7.26). Введение зоны нечувствительности приводит к появлению отрезка покоя и полосы, образованной ли- 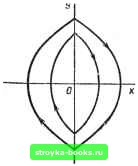 [0] [1] [2] [3] [4] [5] [6] [ 7 ] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] 0.0013 |
|||||||||||||||||||||||||||