
 |
|
Главная Нелинейные системы управления [0] [1] [2] [3] [4] [5] [6] [7] [ 8 ] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] 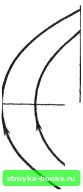 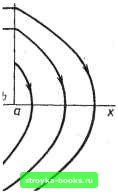 Рис. 7.28 ниями переключения х = а и х = - а, внутри которой отрезки траекторий горизонтальны (рис. 7.27). При наличии гистерезиса процесс расходится (рис. 7.28). Стабилизировать подобную систему можно, охватив релейный элемент отрицательной обратной связью по производной выходной величины. В данной схеме этой производной равна промежуточная координата у = dx/dt, по которой и вводится обратная связь (рис. 7.29). Для случая идеального реле получаем: уЧ2 + kx = С; с = X + ау > 0; уЧ2 - kx С; а = X + а у <: 0. Линия переключения а - х + ау = О (рис. 7.30) представляет собой прямую, проходящую через начало координат и наклоненную к оси абсцисс под углом arctg (-1/а). На -2 j I у=х I ~1 линии переключения мож- но выделить три характерных участка, разграниченных точками касания А и )<: (S0< I В линии переключения с показанными пунктиром параболами. За пределами Рис. 7.29 отрезка АВ фазовая траек- тория по одну, сторону линии переключения после перехода через последнюю является продолжением траектории по другую сторону линии. Внутри отрезка фазовые трактории подходят к отрезку с двух сторон, встречаясь на нем. Попав на отрезок АВ, изображающая точка уже не сможет сойти с него, но не может и остаться на нем. Скорость движения на АВ не определена, но специальные исследования показывают, что она конечна и по значению колеблется вблизи значения ординаты точки. Изображающая точка будет скользить по отрезку к началу координат-точке равновесия типа устойчивого узла. Отрезок АВ называют линией скольжения. Уравнение движения вдоль линии скольжения ау + X = adx/di + х = 0. (7.23) Как видно из уравнения, движение совершенно не зависит от параметров линейной части и определяется только линией переключения, т. е. обратной связью. Это исключительно важное обстоятельство используется при построении многих сисг тем с переменной структурой. На самом деле точное движение по линии скольжения невозможно, оно может иметь место лишь при мгновенном срабатывании реле. Немгновенность его действия приводит к появлению следующих друг за другом с большой частотой замыканий и размыканий, т. е. к появлению высокочастотных вибраций-вокруг линии скольжения. В электрических реле это приво- 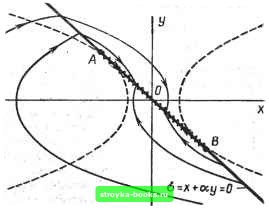 дит к обгоранию контактов. Поэтому вначале после обнаружения скользящих режимов они считались вредными и изыскивались пути их предотвращения. С появлением бесконтактных реле скользящие режимы стали создаваться искусственно с целью обеспечения заданного качества процесса управления при сильно изменяющихся параметрах объекта. Искусственно созданные скользящие движения интересны тем, что закон движения в них определяется не исходными уравнениями, т. е. не параметрами объекта, а параметрами искусственно созданного подпространства скольжения. Системы с переменной структурой позволяют получать ускорение протекания переходных процессов, повышать статическую и динамическую точность управления, противодействовать влиянию внешних и параметрических возмущений. В 1972 г. цикл работ по теории систем с переменной структурой был удостоен Ленинской премии. Многолистная фазовая плоскость. Если характеристика нелинейного элемента неоднозначна, уравнение можно представить как совокупность уравнений с однозначными функциями и каждому из уравнений этой совокупности поставить в соответствие некоторую определенную часть - «лист» фазовой плоскости. Листы эти могут частично накладываться, тогда имеем дело с многолистной фазовой поверхностью. На рис. 7.31 показаны фазовые траектории для уравнений dyldt = 1/Тс при X < е; dyldt = - 1/Гс при л: > - е; dxIdt у. Подобными уравнениями описывается, например, движение объекта первого порядка без самовыравнивания при управлении сервомотором постоянной скорости при наличии зазора 2е между чувствительным элементом и золотником. В этом случае фазовые траектории представляют собой параболы, расположенные на двух листах: лист а соответствует первому уравнению и лист б (заштрихован) - второму. Листы накладываются так, что их оси хи у совпадают. Разрежем листы по линиям переключения А А, ВВ и отрезку оси х и наложим их друг на друга (рис. 7.31, в). Правее линий разветвления А А и ВВ, через которые происходит переход с одного листа на другой, сверху лежит лист б, левее их - лист а. На рисунке сплошной линией показана траектория, начинающаяся в точке М нижнего листа. В полосе - е < л: < е точка может принадлежать обоим листам и, чтобы найти движение, начи- [0] [1] [2] [3] [4] [5] [6] [7] [ 8 ] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] 0.0014 |