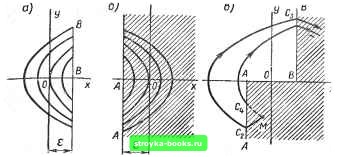Рис. 7.31

кающееся в этой полосе, надо дополнительно указать, какому листу принадлежит начальная точка, т. е. кроме значений х„ и г/о в момент / = О указать также знак производной {dy/dt)o. Так, если точка М лежит на листе а {dyldt при == О положи-тельма), то движение пойдет по линии Мс, показанной пунктиром, поскольку она лежит на нижнем листе, и далее по траектории с, если же точка М принадлежит листу б, то движение пойдет по траектории МсР-

§ 7.5. Метод «припасовывания» граничных значений

Метод «припасовывания», или «сшивания», граничных условий представляет собой точный метод определения процессов в кусочно-линейных системах. Для каждого из линейных интервалов выписывают решение уравнения, в которое входят неизвестные произвольные постоянные. Приравнивая те значения координат и их производных в конце предыдущего и начале последующего интервалов, которые не совершают скачков, находят произвольные постоянные.

Проиллюстрируем метод «припасовывания» на примере нахождения параметров автоколебаний в системе с идеальным поляризованным реле с симметричной характеристикой (7 на рис. 7.6).

Пусть линейная часть системы имеет передаточную функцию W {s) = Р (s)IQ (s), полюсы которой - простые, левые. Степень полинома Р ниже степени Q. Этим исключаются скач-

-2 м

ки координаты х на стыках интервалов. Допустим, что автоколебания существуют и являются простейшими, однопериодными: интервалы включения реле в каждом направлении одинаковы (рис. 7.32).. На интервале / искомый процесс

Рис. 7.32

0<(<.Г/2,

где Sv - полюсы функции \ff (s); Со, Cv - произвольные постоянные; Т - пока неизвестный период автоколебаний; знак минус в формуле указывает на действие отрицательной обратной связи в замкнутой системе. На следующем интервале можно выделить две составляющие процесса. Для этого два последующих включения реле представим как наложение двух сдвинутых на Г/2 ступенчатых функций (рис. 7.32): М-1 (О и -2Л1-1 (-f 7-/2), где М - модуль выходной величины реле, известный из его характеристики. Первая слагающая вызывает продолжение процесса х\ на интервале :

(Н-Г/2)= -С„- 2 Cv

Sv«-l-T/2)

Переменная ? теперь отсчитывается от начала интервала .

Вторая ступенчатая функция вызывает реакцию, которую можно вычислить по формуле Хевисайда:

X (О =2МР (0)/Q(0) + 2М У UlA

Суммарный процесс на интервале ;c..(0=-CoiCve=v(+7/>

v= 1

2МР (0) Q(0)

+ 2М 2

(7.24)

Г, Sv«?(4)

Но в силу симметрии характеристики реле, если однопериод-иые автоколебания существуют, Хи {t) будет равен Xi (f) с обратным знаком:

Хи (t) =-х, {t). (7.25)

Из (7.25) и (7.24) получим

2МР(0) "

(3(0)

СЛеЬ + 1)-

е = 0.

(7.26)

Поскольку равенство (7.26) должно быть справедливым для любых значений t, приравниваем порознь нулю свободный член и множители при eV, v = I, п, тогда

Со=Л1Р(0)/0(0), Cv= ---=-- [1 - th(sr/4)]. (7.27)

Таким образом, все произвольные постоянные выражены через известные коэффициенты и полюсы передаточной функции и через неизвестный период автоколебаний Т. Для нахождения Т составим уравнение периодов, для чего используем условия переключения: на границах интервалов х проходит через нуль.

Для конца интервала /

Подставив Со и Cv из (7.27), получим уравнение периодов в виде

MP ту 2MP(s)-"

ИЛИ после несложных преобразований

(0) + у l![l + th(5,7/4)1 = 0.

Q(0) «(М