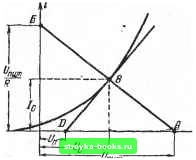Фиг. 18. Графический расчет нелинейной цепи.

Следует заметить, что большинство нелинейных сопротивлений имеет значительный разброс параметров от образца к образцу, тай, что иногда приходится снимать вольт-амперные характеристики именно тех образцов, которые предназначены для использования в данной схеме. В этих

случаях, и ковда для вольтампериой характеристики трудно подобрать аналитическое выр ажение, используют графические методы.

Часто используются также графоаналитические методы, которые и. обеспечивают достаточную точность расчета и в то же время не очень сложны.

Рассмотрим графический метод расчета простейшей электрической цепи, питающейся от источника напряжения постоянного тока и представляющей собой последовательное соединение линейного и нелинейного сопротивлений. Для этой схемы можно написать следующие уравнения:

где и - напряжение источника питания;

г/? -падение напряжения на линейном сопротивлении R;

и - падение напряжения на нелинейном сопротивлении.

Второе уравнение выражает вольтамперную характеристику нелинейного сопротивления. Совместное решение обоих уравнений определит ток i, а следовательно, и величины падений напряжения на каждом из сопротивлений.

Перепишем первое уравнение следующим образом;

пат 1 г л 1 -пат

Полученное выражение на фиг. 18 представляется прямой линией ЛБ, которую часто называют нагрузоч-

дой прямой. Если менять величину R при постоянном значении U, то нагрузочная прямая будет вращаться вокруг точки Л:она будет вертикальна при R = 0 и горизонтальна при R = cx). При изменении величины U и постоянном значении R наклон нагрузочной прямой остается без изменения и прямая перемещается параллельно самой себе.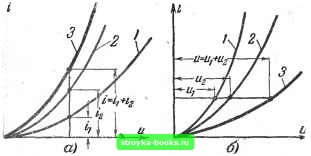

Фиг. 19. Результирующие вольтамперные характеристики (3) при параллельном (а) и последовательном (<?) соедине--НИИ двух нелинейных сопротивлений (/ и 2).

Точка пересечения В нагрузочной прямой с вольтамперной характеристикой называется рабочей точкой. Ее координаты определяют величину тока в цепи г=/(, и падение напряжения на линейном сопротивлении u-Uq. Падение напряжения на линейном сопротивлении также определено, оно равно U - f/p.

Если в электрической цепи имеется несколько нелинейных сопротивлений с различными вольтамперными характеристиками, то их можно привести к одному сопротивлению с соответствующей эквивалентной вольтамперной характеристикой. Это выполняется следующим образом.

Если два нелинейных сопротивления включены параллельно, то суммарный ток равен сумме токов, протекающих через каждое из сопротивлений, а падение напряжения на обоих сопротивлениях одно и то же. Эквивалентная вольтамперная характеристика получается путем сложения ординат вольтамперных характеристик каждого сопротивления при одном и том же соответствующем напряжении, как это показано на фиг. 19,а.

При последовательном соединении нелинейных сопротивлений через них протекает один и тот же ток, а падения 4-J302 49

напряжения складываются (фиг. 10,6). Этот метод можно применить при любом числе последовательно или параллельно соединенных Нелинейных и линейных сопротивлений. Результирующую вольтамперную характеристику используют в дальнейшем для графического расчета всей цепи, как это показано на фиг. IS.

Рассмотренный графическЗий метод расчета применим и для цепи переменного тока в том случае, если нелинейное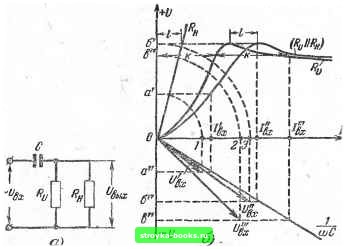

Фиг. 20. Цепь с инерционным нелинейным сопротивлением (а) и ее графический расчет (б).

сопротивление является инерционным. При этом расчет ведется для действующих значений тока и напряжения.

В качестве примера рассмотрим предложенный Г. К. Нечаевым графический метод расчета электрической цепи переменного тока, содержащей реактивное сопротивление и инерционное активное.нелинейное сопротивление вида Rj (термистор). Схема цепи и необходимые графические построения приведены на фиг. 20.

В первом квадранте осей координат f/ и / построены вольтамперные характеристики активных сопротивлений R[j я R, а также их эквивалентная вольтамперная характеристика R II R. В .четвертом квадранте построена

вольтамперная-характеристика конденсатора С, представляющая собой прямую линию.