
 |
|
Главная Цепи и сигналы [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [ 103 ] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] [167] [168] [169] r(t)/n 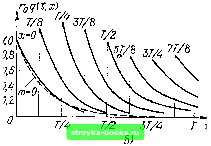 T/ T/2 T t Рис. 10.5. К определению импульсной характеристики цепи, представленной на рис. 10.4 Продифференцировав это выражение по t, можно найти ток i (t). В мо-.мент t = X, когда q {t, х) образует скачок, равный Mr (t), ток будет (1/г (/)) х хб (t - х). Напряжение на емкости можно определить делением выражения (10.25) на Со. Из выражения (10.25) видно, как вариация сопротивления по закону (10.23) влияет на характер разряда: в аргументе экспоненты кроме - (t-x)/ ГдСо (как и при постоянном сопротивлении Гд) появляется периодическое слагаемое {т/гдСа Q) (cos Qt- cos Qx). Закон изменения г {t)/ro показан на рис. 10.5, а, график функции roq (t, х) при rgCgQ = 1 и m •= 0,25 - на рис. 10.5, б. Штриховой линией показана зависимость ехр [-(t-л-)/ГоСо], соответствующая импульсной характеристике при постоянном сопротивлении Го (/п = 0) и л- = б. Для более сложных цепей, описываемых дифференциальным уравнением п-го порядка (п 2), задача определения импульсной характеристики усложняется. 10.4. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ ЦЕПИ С ПЕРИОДИЧЕСКИ ИЗМЕНЯЮЩИМСЯ ПАРАМЕТРОМ Наряду с выражением (10.15) можно дать еще одно определение передаточной функции К (iw, /), которое в некоторых задачах позволяет избежать обращения к импульсной характеристике. С этой целью используем выражение (10.14) для случая, когда входной сигнал является гармоническим колебанием S (t) = cos (Hgt, а соответствующий ему аналитический сигнал г {t)= Спектральная плотность этого сигнала Z (со) = 2яб (со - Ыд) [см. (2.98) и (3.87)1. Подставляя Z (со) вместо S (со) в формулу (10.14), получаем вых (О = - f 2яб (0)-СОо) к (гы, t) е» cio) = К t) e»" 2л J откуда, опуская индекс нуль при о), находим К((ш, 0=2,,,(0/е. (10.26) Под Zgyx (О в данном выражении следует подразумевать аналитический сигнал на выходе цепи при гармоническом воздействии е" на входе. Определение (10.26) особенно эффективно, если передаточная функция К (ico, t) изменяется во времени по периодическому закону. При периоде Т = 2я, Q функцию К (ш, t) можно представить в виде ряда Фурье: К (/со, о - Ко М + Ki (/со) COS (Qt - lx) Ка (гсо) cos {2Qt + У + ..., (10.27) где Ко (tw). Ki (tco),...,- не зависящие от времени коэффициенты, в общем случае комплексные, которые можно истолковать как передаточные функции некоторых четырехполюсников с постоянными параметрами. Произведение Кп (гш) cos (nQt + In) можно рассматривать как передаточную функцию каскадного соединения двух четырехполюсников: одного с передаточной функцией К„ (ioi) не зависящей от времени, и второго с передаточной функцией cos (nQt + in), изменяющейся во времени, но не зависящей от частоты со входного сигнала. Основываясь на выражении (10.27), любую параметрическую цепь с периодически изменяющимися параметрами можно представить в виде эквивалентной схемы, изображенной на рис. 10.6. В соответствии с (10.26), при входном сигнале s (t) = cos со, z (t) = e*, сигнал на выходе будет 2вых (О - К (/со, О е" = Ко (/со) е» + Ki (/со) е" cos (Qt + ei) + + Ка (/со) е» cos {2Qt+ ga) + • • • = Ко Н е <» + р») + Ki (со) е + X X cos (Q/ + 1г) + Кг (со) е «+4=) cos {2Qt + Ы + ... (10.28) Здесь Фо, фь ф2,...-ФЧХ четырехполюсников Ко (/ш), Ki (/со). Кг (tm),... Переходя к вещественному сигналу на выходе, получаем вых (0=Ке2ых {t)=--Ko Н cos (cof Фо) -!- Ki (со) cos (ш< + ф1) cos {Qt+li) + Кг (со) cos (со/ + фа) COS (2Q/ + ia) + • = Ко (<») COS (cut -f фо) + + Т 2 "(со){соя[(со + «0)/ + ф,. + ] + со5[(со-/гО)/ + ф„-„]}. (10.29) Этот результат указывает на следующее свойство цепи с переменными параметрами: при изменении передаточной функции по любому сложному, но периодическо.му закону с основной частотой Q гармонический входной сигнал с частотой m образует на выходе цепи спектр, содержащий частоты т, m + Q, m + 2Q и т. д. s(t) cos(2fif+. I ! I-----1 [ Рнс. 10.6. Схема замещения линейной цепи при периодическом изменении параметров Рис. 10.7. К определению сигнала на выходе параметрической линии задержки
Если на вход цепи подается сложный сигнал, то все сказанное выше относится к каждой частоте © входного спектра. Са.мо собой разу.меется, что в линейной параметрической цепи никакого взаимодействия между огдель-ны.ми ко.мпонентами входного спектра не существует (принцип суперпозиции) и на выходе цепи не возникает частот вида «сох ±- mw, где coj и со, - различные частоты входного сигнала. Поясним при.менение формул (10.26)-(10.29) на примере передаточной функции линии задержки К(гсй. 0= е-"з<) (10.30) при изменении т {() по периодическо.му закону t3(0=To + T„,sinQ Q«(o, (10.31) и при входно.м сигнале s (t) = Е cos cut [соответственно г (t) =- Ee] (рис. 10.7). Основываясь на (10.26), определяем аналитический сигнал на выходе Zeb,x(0 = fe""K(tco, оеС-»--"-"), (10.32) откуда следует s„b,x (О = ReZ3,,, (О -£ cos Гсо (/-То) -сот,„ sin Qtl (10.33) Получилось фазомодулированное колебание с индексом модуляции т - = сотвд и со спектром, аналогичным выражению (3.31). Таки.м образом, коэффициенты ряда Фурье для функции К (ш, t) в данно.м при.мере совпадают с бесселевыми функция.ми J„ (сот) (см. § 3.6). 10.5. ПРИНЦИП ПАРАМЕТРИЧЕСКОГО УСИЛЕНИЯ СИГНАЛОВ В § 10.1 было показано, что по отношению к сигналу, .мало.му по сравнению с управляющи.м колебанием, нелинейная емкость в.месте с генератором накачки .может быть за.мещена линейной, изменяющейся во времени емкостью. Отвлекаясь от способа осуществления модуляции емкости (или индуктивности), можно говорить об обмене энергией между источником сигнала и энергоемким параметрическим элементо.м. Наглядны.м при.меро.м обмена энергией при из.менении емкости является хорошо известная модель с .механическим раздвижением пластин заряженного конденсатора. Пондеро.моторная сила электрического поля конденсатора стремится сблизить пластины (независи.мо от полярности напряжения); следовательно, для их раздвижения, т. е. для уменьшения емкости, необхо-ди.мо произвести работу, которая увеличивает запас энергии конденсатора. При сближении пластин, наоборот, часть энергии поля конденсатора преобразуется в механическую энергию. Рассмотри.м конденсатор (варикап), емкость которого С (t) с по.мощью управляющего напряжения из.меняется по скачкообразно.му закону, представленному на рис. 10.8. Допусти.м, что подобный конденсатор включен в высокодобротнын контур, возбуждаемый сигналом е (t) Е cos о)/, частота которого О) совпадает с резонансной частотой контура ©р = I/VLCq [Со - среднее значение С (t)], а последняя вдвое меньше частоты из.менения C(t). Напряжение на конденсаторе «с (0. близкое к гармоническому, показано на нижней части рис. 10.8. Фаза изменения С (t) подобрана с таким расчетом, чтобы уменьшение емкости происходило в моменты перехода «с (О [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [ 103 ] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] [167] [168] [169] 0.0013 |