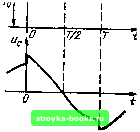Рис. 10.8. Увеличение амплитуды напряжения иа конденсаторе в моменты скачкообразного уменьшения емкости

через амплитудные значения, а увеличение - в моменты прохождения через нуль. В моменты спада С (t) напряжение «с (О получает приращение (см. рис. 10.8), поскольку заряд конденсатора не может мгновенно измениться.

Это означает, что энергия электрического поля в конденсаторе периодически получает приращение, а это эквивалентно увеличению средней мощности сигнала.

Если прирост энергии, обусловленный одним скачком (вниз) емкости С (t), не превышает расхода энергии за время Т, то параметрическая цепь устойчива, в противном случае возникает параметрическое возбуждение колебаний. Таким образом, регулируя относительную величину Ас/Со, т. е. глубину модуляции параметра С, можно осуиествить как параметрическое усиление сигнала, так и параметрическую генерацию.

Реализация скачкообразного изменения С (t) связана с техническими трудностями и в практике не применяется. Значительно проще модулировать емкость по гармоническому закону. Необходимо лишь соблюдать основной принцип: уменьшать емкость в области максимальных значений заряда (напряжения) конденсатора и увеличивать в области минимальных значений.

Дополнительная .мощность сигнала поставляется («накачивается») генератором напряжения, управляющего значением С (t). В связи с этим его часто называют генератором накачки, а управляющее колебание - напряжением накачки.

Управляющее колебание наряду с обозначением е {t) = cos (соу + + у) в дальнейшем часто будет записываться в форме е„ (t) = £„ cos х .x(cd„/+y).

Способ получения периодически изменяющейся емкости поясняется схемой на рис. 10.9, а. К нелинейной емкости С„„ подводится управляющее напряжение накачки Си = Е„ cos ((.o„t + у), наложенное на постоянное напряжение fo-Фильтр Фх преграждает путь току частоты сй„ в цепь источника сигнала, а фильтр - току частоты сигнала со (и близких к со частот) в цепь накачки.

Наложим условие Е < £„. Тогда, как указано в § 10.1, можно пренебречь изменением емкости цод действием сигнала и считать, что закон изменения емкости определяется одним лишь управляющим напряжением. Основываясь на с}юрмуле (10.5"), примем

С(0Со[1-mcos(co„H-Y)l-=Co-ACcos(co„/ + y), /п<1. (10.34)

Рис. 10.9. Воздействие на нелинейную емкость напряжений накачки и сигнала (а) и схема замещения для слабого сигнала (б)

AC = mCo; (10.35)

у - начальная фаза.

На рис. 10.9, б представлена эквивалентная линейная параметрическая схе.ма, на которой цепь накачки не показана.

Определи.м полный ток через емкость С (t) с помощью общего выражения (10.7):

i (t) [Со- АС cos (А„ (у)][ - ыЕ sin at] + Е cos со/со„ АС sin (со„ t -\- у)

- соСо £ sin со/ + Va (ш„ -f- со) АСЕ sin [(а)„ + a)t-]-y] +

+ 1/2(Шн -со) АС£ sinl(m„-т]/ + у]. (10.36)

Частота сон + а :ii За в полосу прозрачности фильтра не попадает; следовательно, ток в цепи источника сигнала является суммой двух токов: на частоте ш и на ко.мбинационной частоте т„ - а, близкой к а (поскольку, ш„ » 2со). Первый из этих токов, сдвинутый по фазе относительно е (t) = = Е cos at на угол 90°, не может создавать активную проводи.мость - ни положительную, ни отрицательную. С точки зрения получения э([х})екта усиления интерес представляет ко.мбинационное колебание разностной частоты oj„ - uj, особенно в частно.м случае ш„ = 2со. При этом ток на частоте о)

Ч-о,,(0--оо(/)= +2 (w„-w)AC£sin[(o)„-u))H-7] - +V2CoAC£x X sin (at + у) = Va соДС£ cos [со/ -f у - л/2]. (10.37)

Амплитуда этого тока = аАСЕ.

При ЭДС источника е (t) = Е cos at и токе /со(/), определяе.мом выражением (10.37), отдавае.мая источником мощность

= -шАС

/72 £2

-sinyGgn -

где символом

соДС

С.к=-

COS у -

/псоСо

Sin у

(10.38)

обозначена эквивалентная активная проводимость, учитывающая расход мощности источника сигнала.

Таки.м образо.м, приходим к схеме замещения (рис. 10.10, б), соответствующей параметрической цепи, показанной на рис. 10.10, а. Комбинационная частота ©„ + m = Зт в этой схеме не учитывается, а частота а - со совпадает с частотой со. В результате по отношению к источнику сигнала параметрическая схема (см.рис. 10.10,сг) приводится к схеме постоянными парамет-ра.ми. Периодическое изменение С (/) с частотой a=2a приводит лишь к появлению активной проводи.мости G, шунтирующей постоянную емкость Со.

Рассмотри.м три следующих характерных режима: у =0, л2 и -л/2 (рис. 10.11). В первом случае (у = 0) С (/) модулируется таким образо.м, что

e(t)

)

а1=сон/2

Рис. 10.10. Параметрическая емкостная цепь (с) и схема замещения для сигнала с частотой, вдвое меньшей частоты накачки (б)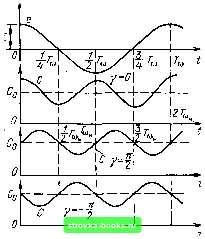

e(t)=E 0036)-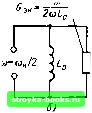

Рис. 10.11. Напряжение на емкости и законы ее изменения при различных начальных фазах

Рис. 10.12. Параметрическая индуктивная цепь (а) и схема замещения сигнала с частотой, вдвое меньшей частоты накачки (б)

изменение запаса энергии в емкости за период колебания Г<,)„ - 2я/о)„ (а также за период = 2л/сй) равно нулю. При этом Оэ„ = 0.

Во втором случае (у = я/2) макси.мальная скорость нарастания С (t) и.меет место в моменты, когда напряжение проходит через .максимумы; при этом часть энергии, запасенной в емкости, переходит в устройство, изменяющее е.мкость. По отношению к источнику ЭДС это равносильно шунтированию постоянной емкости С„ положительной активной проводимостью Gg "= = (m/2) соС,,.

Наконец, в третьем случае, при у = - я/2, когда С (t) убывает в области е {t) Е и нарастает в области е (t) = О, активная проводимость отрицательна: Gg = - (т/2) соС,,.

Этот результат согласуется с результатами приведенного выше качественного рассмотрения принципа параметрического усиления. Отрицательная проводимость Сак учитываст приток энергии от генератора накачки в цепь, содержащую С (t). В данном примере с электронно-управляемой емкостью прирост энергии, запасаемой в емкости, происходит за счет работы, совершаемой генератором накачки при уменьшении емкости (преодоление сил электрического поля при движении электронов и дырок через потенциальный барьер в области запирающего слоя).

Результаты, аналогичные полученным выше для С (/), нетрудно вывести также и для периодически изменяющейся индуктивности L (t).

Исходя из схемы рис. 10.12, а при из.менении индуктивности по закону

L (t) = L„l\ + т cos (со„ + у)\ находим ток с помощью соотношения (10.II) (при m < 1)

(10.39)

(rtZ.„ [I --m cos (m,i / + v)l

E sin Ш

2(0 Z.

(oLn - sin [((0

-m cos (co„ t + y)] sin (iit - E co„)H-Y]

sin at -

2m Lo

(oLo

sin f(co-ш„)-y1