EV2al; М [U (t)] = 2(j + E\ (11.36)

Из последнего выражения вытекает равенство

ст1ых=М [Ut)]-Ul--2al-\-E-Ul (11.37)

Ранее было показано, что в отсутствие сигнала (Е = 0) постоянная составляющая шума на выходе линейного детектора равна Yn/2 [см. (11.18)1.

Приращение постоянной составляющей Ug-Т/л/2ах, где Ug определяется выражением (11.35), и есть полезный сигнал.

Следовательно, отношение мощности сигнала к мощности помехи на выходе линейного детектора

(С/П),, = (t/o -УОхУ/(2а1 + E-Ul). (И-38)

Рассмотрим предельные случаи <g 1 (слабый сигнал) uh I (сильный сигнал).

1. /1 « 1, /„ (hV2) 1, /i {hV2) » /iV4, e-V2 1-i2/2. Выражение (11.35) упрощается:

и о « 1/л72 ах{\+1гЦ1+ И/А)} е- "2 уЧ]2 а„ (1 -f ВД. При этом приращение постоянной составляющей

а дисперсия в соответствии с (11.36)

oLx=2al + E-Таким образом.

а1{1+ hV2f

(11.39)

где d- постоянный коэффициент, близкий к единице.

Выражение (11.39) показывает, что в амплитудном детекторе имеет место подавление слабого сигнала сильной помехой.

Например, при (C/n)x = 0,1 (С/П)» 0,01.

Рассматриваемый вопрос имеет важное значение для проблемы обнаружения сигналов на фоне сильной помехи.

2. /i> 1, функции /о ihV2) и II {W2) можно определять выражениями

. 2 /

Выражение (11.35) при указанных приближениях приводится к виду

t/o « КГо /I (1 -f l/W) =Е (1 + + Е.

Как и следовало ожидать при ЯЗхтж постоянная составляющая выходного напряжения Uq почти совпадаетс Е.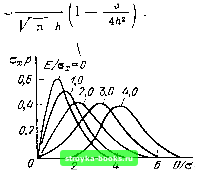

См., например, кривую Е1ох= на рис. 11.9 и комментарий к рисунку на с. 338.

Рис. 11.9. Рэлеевская плотность вероятности (обобщенная)

при вычислении же дисперсии аых необходимо учитывать слагаемое в выражении

Таким образом,

аь,х = 204-£2-(£Но) = а

и отношение сигнал-помеха на выходе

(С/П)„ь,х « Ub/aL. EVol = 2 (С/П),х. (11.40)

Проведем аналогичное рассмотрение для квадратичного детектирования. Заменяя в формуле (П.25) А (t) на U (t), получаем напряжение на выходе квадратичного детектора

"вых (t) = K[EV2 + A (t)/2 + EA (t) cos О (t)]. (11.41)

Усредняя это выражение по времени и учитывая, что (t) = 2о и А {t) cos б (/) =0 (как и среднее значение х (t) = А (f) cos [wgt + 9 (t)], получаем постоянную составляющую напряжения на выходе квадратичного детектора

li::At) К (Е/2+ol)Uoc +и on- (1-42)

Слагаемое t/n - Kl определяет постоянную составляющую, обусловленную помехой [см. (11.27)] в отсутствие сигнала. Слагаемое же 0== = КЕ12, представляющее собой приращение постоянной составляющей под действием гармонического напряжения сигнала, можно рассматривать как полезный сигнал на выходе детектора.

Возводя выражение (11.41) в квадрат, получаем

---4!-1-£Л(/)со5 0(0

+ Е Ait)(J- + - cos 29(t)] + £3 д cos 9 (t) +

+ A (t) E cos e {t)

(11.43)

Слагаемые с cos 9 {t) и cos 29 (t) при усреднении обращаются в нуль. Поэтому средняя мощность на выходе

"вых

(0 =

(/) f (О

4 4

К

-\-2а* + 2Е

Вычитая из этого выражения (иуУ, находим дисперсию шума на выходе квадратичного детектора

oLx = С (EV4 + 2о\ + 2£ oJ)-К (£V4 + Ео\ + oJ) = KE-oloi). (11.44)

При усреднении

М [Л4 (/)] =J 4* р (Л) dA=:8oJ. о

Вследствие эргодичности рассматриваемого процесса в данном параграфе не делается различия между усреднением по множеству и по времени.

При £ = О это выражение переходит в (11.29). Составим теперь отношение сигнал-помеха на выходе детектора (по мощности)

СХ ?с KHF-IA) {EV2olf

(£ 0-t-а*) l-f2£V2a

Но £201 есть отношение сигнал-помеха (по мощности) на входе детектора. Таким образо.м, прн значениях (С/П) С (т- е- при ЕУ2 << al)

(С/П)вь,х « (C/n)L, (11.46)

а при больших значениях (С/П), т. е. при £/2 > о,

(С/П)зь1х «/о.(С/П)нх. (11.47)

Так, при EV2al = 1/10 отношение (С/Пи) == 1/120 [(11.45)1, а при £/20 4 отношение (С/П)вь1х близко к половине отношения сигнала к помехе на входе.

На основании формулы (11.45) можно сделать следующее важное заключение: при слабом (относительно помехи) сигнале в квадратичном детекторе имеет место подавление сигнала, а при сильном сигнале отношение сигнал-помеха пропорционально отношению сигнала к помехе на входе.

Сопоставим результаты, полученные для квадратичного и линейного детектирования. Сравнение формул (11.46) н (11.39) показывает, что при слабом сигнале и сильной помехе линейный и квадратичный детекторы ведут себя одинаково: отношение сигнал-помеха на выходе пропорционально квадрату отношения сигнал-помеха на входе. Таким образом, « в лгшемнол( детекторе имеет место подавление слабого сигнала. Анализ показывает, что это свойство присуще детекторам и с любыми другими вольт-а.мперньши характеристиками.

Однако при Е Ох отношение сигнал-помеха на выходе квадратичного детектора в 4 раза (по мощности) меньше, чем у линейного [ср. (11.47) и (11.40)1. Это объясняется тем, что при квадратичном детектировании сильный сигнал выносит помеху на участок характеристики с повышенной крутизной, что приводит к относительному увеличению помехи. Действительно, пусть огибающая амплитуд входного напряжения, равная 1 В, получила приращение в результате наложения помехи о< 1. Тогда напряжение на выходе квадратичного детектора в соответствии с (11.25) увеличится от 1(/2 до (К/2) (1 + а) {К/2) (1 + 2а), т. е. относительное приращение (помехи) будет 2а, а при линейном детектировании это приращение будет всего лишь а. Переходя от напряжения к мощности, получаем проигрыш в 4 раза.

Хотя проведенное рассмотрение относится к гармоническому (немоду-лированному) сигналу, полученные выводы можно полностью распространить на обработку прямоугольных импульсных радиосигналов на фоне помех, когда импульс на выходе детектора есть приращение постоянной составляющей выпрямленного напряжения в промежутке времени, равном длительности импульса.

Наличие амплитудной модуляции сигнала, которую .можно рассматривать как медленное изменение постоянной составляющей напряжения на выходе детектора, также не оказывает существенного влияния на сравнительную оценку (С/П)вцх при квадратичном и линейном детектировании.

Следует, наконец, отметить, что все полученные в этом параграфе результаты не зависят от соотношения между несущей частотой сигнала со,, и мгновенной частотой помехи + 9. Из этого следует, что наложение пара-