получаем

.-«1тг1

cos шо т.

(11.72)

Находим теперь энергетический спектр с помощью выражения (11.68):

; (М)

cos ш о те

-CXJ

- no - ОО

ОО ОО

Первые два интеграла дают дельта-функции 2пб (ы - Wq) и 2я6 (ы -г w„). Последние же два интеграла дают соответственно 2а/[а Н- (w - й>„)] и 2а/[а -f (ы -1~

+ 0)о)2].

Таким образом, окончательно

Ь (<» - шо)

а - (со -С1)„)2

(11.73)

Функция йвых (С") изображена на рнс. 11.13. Монохроматической составляющей выходного сигнала соответствуют две дискретные спектральные линии, а шумовой сос-ставляющен, обусловленной флуктуациями усиления АК (t),- сплошной спектр (на рис. 11.13 заштрихован). Этот спектр состоит из комбинационных частот, располагающихся симметрично относительно частоты сигнала coj (в области отрицательных со симметрично относительно - со„.).

2. Гауссовский случайный процесс s (t) с нулевым средним и со спектром ( рис. 11.14)

tts(0))=2c/;(6-~<J)-).

пирующимся вблизи цией

К {П = Л„ (I -f- -И co.s at). М < I.

(11.74)

группирующимся вблизи нулевой частоты, действует иа входе цепи с передаточной функцией

(11.75)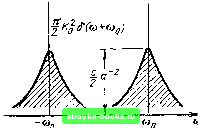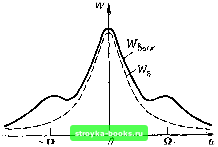

Рис. 11.13. Спектр на выходе параметрической цепи со случайной передаточной функцией при гармоническом воздействии

Рис. 11.14. Спектр на выходе параметрической цепи с передаточной функцией, изменяющейся по гармоническому закону, прн воздействии гауссовского процесса

Находим корреляционную функцию входного сигнала

- оо

и ковариационную функцию цепи

К (X) = Kl + 4iMK cos Qx. (11.77)

Тогда в соответствии с (11.66) корреляционная функция выходного сигнала «вых (т) = /С, (т) ;?Лт) = (/С? + Y cos Qt j е - ll (11.78)

и спектр

оо оо

вых(ш) = уК§ j e-lle-"dT+ "J f e-WcosQTe-"dT =

= Kl-7r-T+KbMd

62 + 0)2 " ft2 ( Qj2 63 .(o)--Q)2

(11.79)

функция Wbux (сй) изображена на рис. 11.14.

3. Нормально распределенный случайный процесс s {t) действует на входе цепи, передаточная функция К (О которой является также случайным процессом с нормальным распределением.

Спектры процессов s (t) п К (t) зададим в форме Wg (ш) = 2d/ (Ь + о)2) - - как в примере 2, (м) = 2п /Соб(м) + 2с/{а + ы) - как в примере 1.

Корреляционные функции входного сигнала и рассматриваемой цепи соответственно

«s(T)=-je-"l. Кк{х)=К1+е-К Находим корреляционную функцию выходного сигнала

W (т) =/Ск (t) Rs (x) = ~Kl е-Ч- -MW (,,.80)

и спектр

2d cd 2{a + b)

о2 + о)2 ао [(0 + 0)2 4-0)2]

Первое слагаемое в правой части соответствует сигналу на выходе цепи с передаточной функцией Ко (в отсутствие мультипликативной помехи), а второе слагаемое соответствует мультипликативной помехе. Значение этого слагаемого пропорционально произведению параметра d, характеризующего интенсивность сигнала, и параметра с, который определяет дисперсию флуктуации передаточной функции цепи а.

11.9. ВЛИЯНИЕ МУЛЬТИПЛИКАТИВНОЙ ПОМЕХИ НА ЗАКОН РАСПРЕДЕЛЕНИЯ СИГНАЛА .

Рассмотренные в предыдущем параграфе характеристики случайного сигнала - корреляционная и спектральная - не являются исчерпывающими. Для прикладных задач большой интерес представляет определение плотности вероятности р (sx)-

В общем случае, когда передаточная функция цепи К (i, at) является функцией двух переменных - частоты и времени, отыскать р (Sgux) при произвольном законе распределения входного сигнала весьма затруднительно. Задача значительно упрощается при мультипликативной помехе типа AM, когда передаточная функция К {t) зависит только от одной переменной - времени t.

Имея в виду это условие, рассмотрим следующие три характерные ситуации:

1) S (t) - случайный, /( (t) - детерминированный процессы;

2) S (t) - детерминированный, К(() - случайный процессы;

3) S (t) и К (О - случайные процессы.

Ситуации 1) и 2) приводят к задаче нахождения закона распределения произведения s (t) К (t), в котором один из сомножителей является случайной, а другой - детерминированной величиной. Если случайный процесс стационарный, задача легко решается. Из теории случайных функций известно, что при умножении случайной функции х (t) (стационарный процесс) с дифференциальным законом распределения р (х), с нулевым средним и дисперсией а на детерминированную функцию времени у (t) получается нестационарный процесс х (t) у (t) с прежним законом распределения, но с дисперсией аых = 1 У (О-

В частности, если входной сигнал s (t) - стационарный гауссовский процесс с дисперсией а, а передаточная функция системы К (t) - детер.ми-нированная (случай 1), то выходной сигнал сохраняет нормальное распределение, однако каждому фиксированному моменту времени соответствует своя дисперсия аых = о» (О-

При детерминированно.м сигнале s (t) и случайной функции К (t) (случай 2), если последнюю можно представить в форме К (О = /Со + А/С (0. выходной сигнал целесообразно записать в виде

«вых (О = K{t)S it) = Ko S (t)+AK it) S (0 ==5зых дет (О+ых сл (t)-(1 1 -82)

Первое слагаемое в правой части характеризует полезный выходной сигнал (детерминированный), а второе - мультипликативную помеху (случайную). Закон распределения этого слагаемого такой же, как у случайного процесса АК (i), но с дисперсией (t) (при АК (О = 0).

Рассмотрим случай 3). Пусть оба процесса s (t) и К (t) стационарные, с плотностями вероятности соответственно р (s) и р (К). Задача заключается в нахождении плотности вероятности случайного процесса Sj,bix (О, являющегося произведением s (i) п К (О-

Из теории вероятностей известно, что если взаимно независимым случайным величинам х и у соответствуют плотности вероятности р (х) и р (у), то произведению z - ху соответствует плотность вероятности р (z), определяемая выражением

p{z)= Г pix)pi±.]-J. (11.83)

J. \ x j \х\

- оо

Подразумевая под х входной сигнал s (/), под у передаточную функцию К (0. а под Z произведение хцх (О = s (t) К (t), получаем выражение для определения плотности вероятности выходного сигнала Sgj.

Проиллюстрируем применение (11.83) на примере передачи гармонического сигналах = А„ cos{(i>t 6), в котором начальная фаза 9 является случайной величиной, равномерно распределенной на интервале (-л, я), через линейную цепь с передаточной функцией К (0> флуктуирующей относительно среднего значения Ко по нормальному закону.

Таким образом, соответствующие плотности вероятности

P(s) =-/ -Ao<s<Ab,

nVAl-s