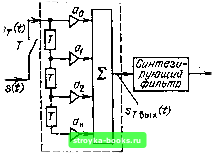Рис. 12.2. Дискретный фильтр

Рис. 12.3. Импульсная дискретного фильтра

характеристика

Для схемы на рис. 12.2 числа g (kT) совпадают с весовыми коэффициентами фильтра flft.

Запишем выражение (12.2) в форме

sximT) У s[{m-k)T]g{kT) s{kT)g[{m-k)T]. (12.3)

Выражение (12.3) является дискретным эквивалентом интегральной свертки (см. § 6.3), используемой при анализе прохождения континуальных сигналов в аналоговых цепях.

Представленную на рис. 12.3 импульсную характеристику gr (t) можно трактовать как результат дискретизации с шагом Т континуальной импульсной характеристики соответствующего аналогового фильтра. Сигнал, выделяемый на выходе синтезирующего фильтра в схеме на рис. 12.2, совпадает с сигналом на выходе указанного аналогового фильтра.

Представленный на рис. 12.2 фильтр иногда называют трансверсальным (поперечным). Возможности фильтра значительно расширяются при введении цепей обратной связи (рис. 12.4).

При наличии обратных связей значение сигнала на выходе сумматора в любой момент времени тТ зависит не только от Н отсчетов входного сигнала, но и от некоторого количества отсчетов вьаодного сигнала в предшествующие моменты. Подобные фильтры называются рекурсивными. Для такого фильтра разностное уравнение (12.1) следует заменить более общим уравнением, учитывающим обратные связи с весовыми коэффициентами bi, bi, Ьм-

5вых (тТ) До S (тТ) + а s (тТ - Г) + s (тТ - 27) + ... -f + ан S (тТ -ИТ) + sx {тТ-Т) + smx (тТ-2Т) +... +

(12.4)

Принципиальное различие между трансверсальным и рекурсивным фильтрами заключается в свойствах их импульсных характеристик. В первом случае импульсная характеристика содержит конечное число отсчетов (не превышающее Н), а во втором благодаря обратной связи число отсчетов теоретически бесконечно велико. В связи с этим трансвер-сальные фильтры иногда называют КИХ-фильтрами, а рекурсивные- Рис. 12.4. Цифровой фильтр с обратными БИХ-фильтрами, связями

+ Ьм8,АтТ-МТ).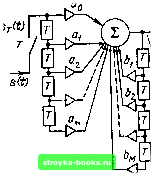

Синтезирующий фильтр

12.3. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ ЦИФРОВОГО ФИЛЬТРА

Дискретный сигнал, действующий на входе цифрового фильтра, удобно представлять в форме, аналогичной (2.122), но с учетом начального условия S {кТ) = Оприк<:0:

sr(0- 5 s{kT)8{t-kT).

Соответственно изображение, по Лапласу будет [см. (2.125)1

L[sr(t)] = s{kT)e-pL . (12.5)

<г = 0

Нетрудно составить аналогичное выражение для дискретного сигнала на выходе фильтра.

В случае трансверсального фильтра результирующий сигнал на выходе сумматора можно записать в виде суммы

5гвых (/) = Оо Sr (О + aiST{t-T) + ... + aHSr(t~HT).

Применив к этому выражению преобразование Лапласа, с учетом теоремы смещения получим

Ь[5гвых1 = 5гвых(р) = 5г(р) 2 ае-Р*?-.

Передаточную функцию цифрового фильтра в общем виде определим отношением

Кг(я) = 5гвых(/с)/5г(р). (12.6)

Для трансверсального фильтра это отношение будет

Кг (р) = «о + «1 е- + «2 е-Рт- +... + а„ е-р"т. (12.7)

Заметим, что выражение (12.7) можно также получить, применив преобразование Лапласа непосредственно к импульсной характеристике g (kT), представив ее в форме

Действительно,

L [gT(t)] = flo + Oi e-P-f 02 e-Pr + „+a„e-P" Кт{р). (12.8)

Итак, импульсная характеристика и передаточная функция цифрового фильтра, как и в случае аналогового фильтра, связаны между собой преобразованиями Лапласа и Фурье.

Подставив в (12.7) р = ш, получим передаточную функцию на оси частот

Kr(tw)= 2 Ofte-*-. (12.9)

Сопоставление выражений (12.9) и (2.124) показывает, что передаточная функция цифрового фильтра Кг (ш), как и спектры Sr (ы), 5гвых (й), имеют периодическую структуру с периодом (на оси частот), равным 2п/Т.

12* 355

1 j/cra>.2;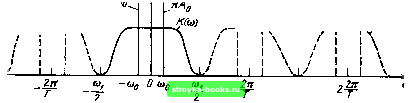

------

Рис. 12.5. Амплитудно-частотная характеристика дискретного фильтра

Следовательно, передаточную функцию дискретного фильтра наряду с с (12.9) можно записать также в форме

Кг (И- 2 Ка

I (О-Л

(12.10)

где Кан (iw) - передаточная функция аналогового фильтра, обладающего импульсной характеристикой g \t), которая соответствует дискретной характеристике gr (t) (см. замечание в конце предыдущего параграфа).

Выражение (12.10) аналогично выражению (2.123). Если шаг Г мал по сравнению с протяженностью функции g (t) или, что то же самое, частота повторения щ = 2л/Т больше полосы прозрачности фильтра, то частотные характеристики, соответствующие разным значениям п, не перекрываются. В этом случае на центральном участке - (jiJ2<; (о<; (ui/2, т. е. при л = О, характеристики Кг (iw) и Кан (iw) полностью совпадают. Это иллюстрируется рис. 12.5. для дискретного фильтра нижних частот при воздействии гармонического колебания s (t) - cos (Hgt со спектральной плотностью пАд [S (со - (Оо) -4- б (ю -f (Ор)] [см. (2.98)]. Сплошными линиями показан спектр до дискретизации, а штриховыми - периодическое продолжение этого спектра.

Амплитудно-частотная характеристика фильтра в центральном интервале показана также сплошной линией. После обратного преобразования дискретного сигнала 5гвых (О в континуальный сигнал sx (О (с помощью СФ, см. рис. 12.2) только этот частотный интервал и определяет спектральный состав выходного сигнала.

Следует подчеркнуть важность этого заключения. По существу оно означает, что определение передаточной функции дискретного фильтра как отношения Згвых (w)/Sr ((о) можно распространить и на отношение S <;Твых(»)/ /S ((о). Иными словами, выражение (12.6) можно трактовать как передаточную функцию дискретного фильтра в целом с учетом как процесса дискретизации сигналах (t) на входе, так и восстановления континуальной формы Sgbix (О на выходе устройства.

Определим теперь передаточную функцию рекурсивного цифрового фильтра. Повторяя рассуждения, приведшие к формуле (12.7), и учитывая разностное уравнение (12.4), приходим к следующему уравнению:

5гвых (О = «о St (t) + fll Sr it - Л ¥ «2Sr (/-27) + ... + + ая Sr {t-HT) + fei 5гвь,х (-Г) + 2 5гвых [t-27) 4--\-Ьм8Твик (t-MT).

...+