Применив к этому уравнению преобразование Лапласа, получим

8гвь,х (р) St (р) (Оо + а, е-" -Ьо., с-р -f ... +a« е-рО Ч-+ Sr„b,x (р) е-р+бг е-" ! ...+Ьм е-),

откуда следует, что Кг(р) =

рНТ

- .., - йд, е

(12.11)

Здесь Н - число суммируемых предшествующих входных, а М - предшествующих выходных отсчетов.

Полученную функцию можно трактовать как передаточную функцию каскадного соединения двух фильтров: одного с передаточной функцией

ат(р) V е-" и второго с передаточной функцией

hiP)

Таки.м образом. Кт(р)==ост(р)Рт(Р)-

Перейдя от переменной р к /(о, запишем передаточную функцию рекурсивного фильтра

Кг (т) =

(12.12)

Такому представлению соответствует каноническая схема на рис. 12.6. Каждый элемент памяти Т в этой схеме используется как для цепи прямой связи (с весовым коэффициентом а), так и для цепи обратной связи (с весовым коэффициентом /;„). Поэто.му общее число элементов памяти Т вдвое меньше, чем в схеме на рис. 12.4. Легко убедиться, что разностные уравнения (12.4) справедливы и для канонической схемы.

Рис. 12.6. Каноническая схема цифрового рекурсивного

фильтра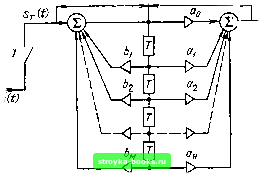

12.4. ХАРАКТЕРИСТИКИ ЦИФРОВЫХ СИГНАЛОВ

В § 2.17 было показано, что спектральная плотность S-,- (oj) дискретизованного по времени сигнала s (t) имеет периодическую структуру с периодом на оси частот щ = 2п/Т (рис. 12.7, б). Как и спектр S (со) исходного (континуального) сигнала (рис. 12.7, а), Sj («) - сплошной спектр. Между тем для осуществления цифровой обработки требуется дискретизация сигнала не только во временной, но и в частотной области. Это означает, что сплошной спектр S?- (со) должен быть представлен совокупностью своих значений Sr (пАсо) на дискретных частотах oj = nAoj. Подобный спектр, показанный на рис. 12.7, в, получается из сплошного спектра Sr (oj) при периодическом повторении последовательности (s (kT)} с периодом Т. = = NT. В соответствии с § 2.7 интервал между соседними спектральными линиями Асо = 2л/Ге 2n/NT.

Обращаясь к выражению (2.124)

Sr(co)= V 5(йГ)е

*= о

и подставляя со пАы, получаем следующее соотношение:

,4-1 .V- 1 -7""

- V S (/гГ) е , n = 0,±\,...,±N2

8г{пАы}- V s(kT)e

(при четном Л).

Полученное выражение называется дискретным преобразованием Фурье (ДПФ).

Аргументы лАсо и кТ обычно обозначаются просто п и k. Поэтому ДПФ можно записывать в (юрме

S(n) = v s{k)e

. 2л

. .« = 0, ± 1,..., ±N.2.

:i2.i3)

s(t)

ОТ кТ NT sCA)

о/гз

S(cj)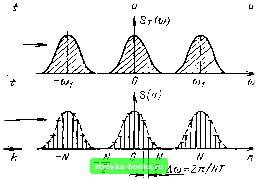

Pile. 12.7. Дискретизация сигнала но времени и по спектру:

(/) континуальный сигнал s(r) и его спектр .S(<i)): б) .анскретнзованный сигнал (/) и его спектр (сплошной); в) периодическая моследовательиосгь /s(*)) с периодом .V и ДПФ S(n))

Выражение (12.13) можно трактовать как алгоритм вычисления спектральных коэффициентов {S (л)} по заданным временным отсчетам {s (k)}.

При четном Л и действительном s{k)

S{N/2 + l) = S*(N 2-1), 1 = 0,1,..., N/2,

где S* (л) - величина, комплексно-сопряженная S (л).

Действительно, подставляя в S (п) п - N12 + / и учитывая, что N является периодом, получаем

-4 -3 -2 -f

0 1 2 3 и„ 5 О Лы г&ыЪАы Лы

6 7 Ъ п

4 б)

01ZZU5 67 bn Ы)(-Ю(-2)Н) (0)

Рис. 12.8. Нумерация спектральных коэффициентов при четном N

л -1

V s(fe)e

= S*

/ = 0, 1,..., N12,

что и требовалось доказать.

Из последнего равенства, в частности, следует, что при / = О S (jV/2) = =- S* (Ni2), т. е. что S (Л"2) - всегда действительное число. Это справедливо и для S (0).

На основе доказанных свойств ДПФ картину образования периодической структуры спектра можно пояснить построением, показанным на рис. 12.8 (для Л = 8). Амплитудный спектр исходного континуального сигнала представлен на рис. 12.8, а. Весь диапазон разбит на равных интервалов Асо. Отсчетные точки на оси частот расположены в середине каждого из интервалов. На рис. 12.8, б представлено периодическое продолжение спектра. В точке л = N12 = 4 5 (4) = 5 (-4) - действительное число, в точке л •= 5 = N12 Л- 1 спектральная плотность S (5) = S* (3), а по модулю S (5) = S* (3) и т. д. При п 8 = N начинается новый период последовательности S (л). Очевидно, что в пределах одного периода выражение (12.13) можно записывать в форме

S(«)= V s(fe)e , п = 0,1,..., N- \. (12.14)

Именно в такой форме в дальнейшем будет записываться ДПФ последовательности временных отсчетов.

Введем понятие обратного дискретного преобразования Фурье (ОДПФ). Используя дуальность прямого и обратного преобразований Фурье, можно, основываясь на выражении (12.14), записать

. 2л

.\- 1

s{k) -С V S(n)e