2.9. РАСПРЕДЕЛЕНИЕ ЭНЕРГИИ В СПЕКТРЕ НЕПЕРИОДИЧЕСКОГО СИГНАЛА

Для получения выражения, аналогичного (2.42), .можно идти двумя путями: исходя из (2.42) совершить предельный переход Т -> оо или воспользоваться результатами предыдущего параграфа.

Рассмотрим второй путь. Для этого воспользуемся выражением (2.63).

Если f (t) и g (t) представляют собой одно и то же колебание

/ (О g (О - S it), то интеграл

\ f{t)g(t)dt= \ s(t)dt3

- оо --ОС-

представляет собой полную энергию сигнала s (t). Кроме того, произведение спектоальных плотностей G (со) и F* (со) приводится к виду

G (ш) F* (со) =- S (со) S* (со) = 1 S (о)) \ = (со),

где S (ш) - спектр сигнала s (t), а S (со) - модуль этого спектра.

Таким образом, в соответствии с (2.63) приходим к окончательному результату

X V V

Э= J 50/= j lS(c«)f dco = - j" S-(co)dco. (2.66)

Это важное соотношение, устанавливающее связь между энергией сигнала и модулем его спектральной плотности, известно под названием ра-венства Парсеваля.

Между выражениями (2.42) и (2.66) имеется существенное различие. В § 2.5 речь шла о средней мощности периодического колебания. Операция усреднения осуществлялась делением энергии отрезка колебания за один период на величину Т. Для непериодического колебания конечной длительности усреднение энергии за бесконечно большой период дает нуль и, следовательно, средняя мощность такого колебания равна нулю.

Важно отметить, что энергия непериодического сигнала не зависит от фазировки спектральных составляющих. Это является, как и для периодического сигнала, результатом ортогональности спектральных составляющих. Различие заключается лишь в интервалах ортогональности: период Т для периодического сигнала и бесконечно большой интервал для непериодического сигнала.

Из выражения (2.66) видно, что величину S (со)-, имеющую смысл энергии, приходящейся на 1 Гц, можно рассматривать как спектральную плотность энергии сигнала.

2.10. ПРИМЕРЫ ОПРЕДЕЛЕНИЯ СПЕКТРОВ НЕПЕРИОДИЧЕСКИХ СИГНАЛОВ

Основной задачей настоящего параграфа является пояснение свойств преобразований Фурье, приведенных в предыдущих параграфах, на примерах, важных для практики.

1. ПРЯМОУГОЛЬНЫЙ ИМПУЛЬС Простейшее колебание, определяемое выражением А при - т„/2<<т„/2, О при т„/2 и >т„/2

(2.67)

и представленное на рис. 2.14, а, получило широкое распространение как в технике, так и в теории сигналов и цепей. Применяя формулу (2.48), находим спектральную плотность (рис. 2.14, б)

(ИТ,.

Si (со) = л J

2А (ОТ, -Sin

sin (а)Ти/2) (от„/2

(2.68)

Заметим, что произведение Лт, равное площади импульса, определяет значение спектральной плотности импульса при со = О, т. е. Sj (0) == Лт„ [см. (2.55)].

Таким образом, выражение (2.68) можно записать в (}юрме

Si (со) =Si (0) i"("H/2) (0) sine f-i V (2.69)

(от„/2 I 2 у

Здесь через sine (сот„/2) обозначена функция

sine (х) = (sin х)/х. - (2.70)

При удлинении (растягивании) импульса расстояние между нулями функции Si (со) сокращается, что равносильно сужению спектра. Значение Si (0) при этом возрастает. При укорочении (сжатии) импульса, наоборот, расстояние между нулями функции Si (со) увеличивается (расширение спектра), а значение Si (0) уменьшается. В пределе при т„ -0 (Л = const) точки 0)1 = ±2л/т„, соответствующие двум первым нулям функции Si (со), удаляются в бесконечность и спектральная плотность, бесконечно малая по величине, становится равномерной в полосе частот от -оо до оо.

На рис. 2.15 показаны отдельно графики модуля Si (со), отнесенного к величине Si (0), и аргумента Э (со) спектральной плотности. Первый из этих графиков можно рассматривать как АЧХ, а второй - как ФЧХ спектра прямоугольного импульса. Каждая перемена знака S (со) учитывается на рис. 2.15, б приращением фазы на л.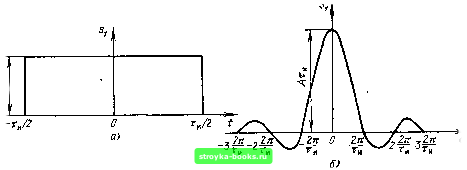

Рис. 2.14. Прямоугольный импульс (а) и его спектральная плотность (б)

-3n-Zn -n 0 ft ZtT 3Tt wrJ2 \ \ \ Ь

Рис. 2.16. Совмещение начала отсчета времени с фронтом прямоугольного импульса

Рис. 2.15. Модуль (а) и аргумент (б) спектральной плотности прямоугольного импульса

При отсчете времени не от середины импульса (как на рис. 2. 13), а от фронта (рис. 2.16) ФЧХ спектра импульса должна быть дополнена слагаемым о)т„/2, учитывающим сдвиг импульса на время т„/2 (в сторону запаздывания). Результирующая ФЧХ принимает при этом вид, показанный на рис. 2.15, б штриховой линией.

2. ТРЕУГОЛЬНЫЙ ИМПУЛЬС Представленный на рис. 2.17, а импульс определяется выражением

J .fl\--liL/O,

т„/2 ; 2 (2.71)

«2(0-

т„/2 У 2

Прямое вычисление спектральной плотности треугольного импульса по формуле (2.48) хотя и несложно, все же несколько громоздко.

Для иллюстрации применения теорем о спектрах, приведенных в предыдущем параграфе, найдем сначала спектральную плотность функции, являющейся производной от заданного сигнала Sj {t). График производной показан на рис. 2.17, б. Спектральная плотность положительного прямоугольного

импульса длительностью t„/2 и амплитудой -rj- по аналогии с формулой

(2.68) и с учетом сдвига середины импульса на время t„/4 относительно точки О

til sin ((оТи/4) g-f-(-(0x/4 2 сот„/4

- Д sin (а)Ти/4) g(-wT„/4 шт„/4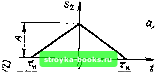

Рис. 2.17. К определению спектральной плотности треугольного импульса 38