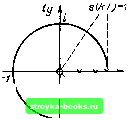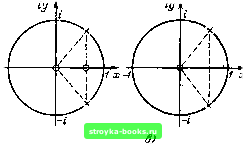ffj sCkDa" 6)

Рис. 12.11. Положение нулей и полюсов на z-плоскости для: а) s(ltT) = \. е-и е»*"; б) s(АГ)-cos и»*7"; в) sCfejsin Ю(,*Г

Нуль Zo = 0, ПОЛЮС Zn = a, Го=а", zl>e-«".

4. Последовательность отсчетов из сигнала s{t) - cos (x)„t, fO.

В этом случае s(T) =-е"«*+ -i-е -и

S(z)= у cos(Ooyfer-z-*=-i- V (e<oVz-i)* +

/!=0

22 (1 е--1) + (1-е»»г-1)

2 1 е-"«г-1 г (г-cos (Оо Г)

22 -2г С05(ОоГ+1

22-2г cosaoT-f 1

(12.24)

Нули Zqi = О, = cos (Од Т, полюсы Zni,2 = cosЫдТ ±isin сОд7, 1г„ =1; Гд=1, z>l.

5. Последовательность отсчетов из сигнала s(t)- s{n(cigt, fO. В этом случае s (jfeT) =-у-е"»*-J e-«»fe7" и

оо 00

S(z)=: V sin(o„feT-z-* =- V (e<.7-z-i)* -

J 2(e-.z-r = -J

2 .=0 г sin (Oo Г

22 - 22 cos (ОоГ-fl

(12.25)

Нуль Zo = 0, полюсы Zj,i,2 = cos (OqT ± I sin (i>qt;\z„\ =1; Гд =1, iz> 1.

Положение нулей и полюсов для приведенных выше пяти сигналов показано на рис. 12.11.

Отыскание оригинала, т. е. функции St (t), no заданному изображению

S (z) производится с помощью обратного z-преобразова-н и я, которое получается подстановкой еР = z в обратное преобразо-

вание Лапласа. Основываясь на выражении (2.127) и подставив в него St- {р) == S (z), е"*, = z* и d;? = dzlTz, получим

s{kT)T-±r § S(z)z±..±- § S(z)z(-nd,. (12.26)

Интегрирование ведется по окружности радиуса г = е, в которую преобразуется прямая о - с из плоскости р = а -\- /со. Постоянная с определяется из условия, что все полюсы подынтегральной функции находятся внутри круга радиуса г = е. Обход контура - в положительном направлении (против часовой стрелки). Изменению частоты от - л/7 до л/7 соответствует один обход окружности.

В рассмотренных выше примерах функций S (z), обладающих полюсами на окружности единичного радиуса [при s {kT) = 1, cos (nkT и sin (nkT], постоянная c:> 0 может быть сколь угодно малой. Поэтому контур интегрирования можно свести к окружности радиуса г = \ с обходом полюсов вне круга, подобно тому, как на плоскости р = а -\- ш интегрирование ведется по оси ш с обходом полюсов, лежащих на этой оси, справа.

С учетом этого условия выражение (12.26) можно записать в (}х)рме

s(fe7)r:r i- фS(z)z(*-i)dz. (12.27)

™ гГ=1

Интегрирование по окружности г > 1 из дальнейшего рассмотрения исключается, поскольку положение полюсов функции S (г) вне круга г = 1 соответствует неограниченно возрастающим временным последовательностям, не имеющим физического смысла.

Заметим, что при интегрировании по окружности z = 1 имеет место равенство z = е"*, что позволяет с помощью соотношения dz = /7е" do) привести выражение (12.27) к виду

s(fe7) = - j S(e0e""rf(«7). (12.28)

Сопоставим z-преобразование с ДПФ для последовательности s {kT), k = 0,1, - 1. Для этого воспользуемся выражением (12.20) для зна-

чений функции S (z) в точках z = е" = е :

. 2л . 2я ,

е j= 2 s(e , п = 0, 1,...,/V -1. (12.29)

/е=0

Правая часть этого выражения полностью совпадает с выражением (12.14), из чего следует, что спектральные коэффициенты S {п), т. е. ДПФ последовательности {s {k)}, k - 0,1, - 1, равны значениям z-npe-

образования этой последовательности в N точках, равномерно распределенных по единичной окружности.

Поскольку при использовании метода z-цреобразования имеется в виду однократный обход единичной окружности, то обратное г-преобразование по формуле (12.28) обеспечивает однозначное определение элементов конечной последовательности (s {k)}, k = 0,1, N - 1.

Напомним, что обратное ДПФ по сюрмуле (12.15) приводит к периодической последовательности {s {k)} с периодом N даже при конечной исходной последовательности {s (k)}

12.7. z-ПРЕОБРАЗОВАНИЕ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ ДИСКРЕТНЫХ ЦЕПЕЙ

Применим z-преобразование к передаточной функции дискретной цепи. Подстановка е г в выражение (12.11) дает

у: а, г-"

К (2)--- вь.х(г) -. (12.30)

S{2) , уб,г-

к- I

Из этого выражения видно, что передаточная функция дискретного фильтра является дробно-рациональной. По заданному выражению (12.30) легко составить разностное уравнение вида (12.4), определяющее алгоритм преобразования входной импульсной последовательности в выходную. Для этого каждому из слагаемых вида s \{т - k) Т] в уравнении (12.4) достаточно приписать коэффициент при степени г-* в числителе, а слагаемым вида Sgx [(т. - k) Т\ - коэффициент bh при степени z-* в знаменателе выражения (12.30). Соответственно по заданному разностному уравнению можно составить выражение (12.30).

Следует, однако, отметить, что не всякая дробно-рациональная функция может быть реализована в виде передаточной функции фильтра. Пусть, например, передаточная функция задана в виде отношения полиномов по положительным степеням

Разделив числитель и знаменатель на Ьп z, приведем это выражение к виду

К(г) =

- 7 -f- --- 7 -4- ... - - Z

г- - . . . -- г

Если Н > М, то первое слагаемое в числителе (с положительной степенью г) образует в уравнении (12.4) слагаемое вида (йо/о) « U" + k)T\, где k ~ Н - .И > О, соответствующее импульсу s {т + k), опережающему во времени входной импульс s (m), что, конечно, невозможно. Отсюда следует, что фильтр осуществим при условии, что степень знаменателя в (12.31) больше или равна степени числителя.

С учетом этих замечаний запишем передаточную функцию в следующих эквивалентных формах (при б,, = 1);

К(г) = -

г-"(««","--г«."~--...Ч"л,)

(12.32)

К (,) ,м-н (-о.)(г-Зо.)...(2-го,)