Рис. 12.17. Амилитудно-частот-ные характеристики рекур- iO сивного фильтра (рис. 12.13)

" 0,1 0,2 0,Ъ 0,i4 0,5 0,5 0,7 0,& ы/а

Это выражение получается последовательным обходом кольца обратной связи.

Импульсная характеристика при 6i > О показана на рис. 12.16, а, при 6i< О - на рис. 12.16, б.

При любом знаке bi для устойчивости цепи должно выполняться условие 1 6, j < 1 [см. пояснения к (12.33)1.

Передаточная функция определяется по формуле (12.30):

K(z) =

(12.47)

Эту же функцию можно представить в форме геометрической прогрессии

K(z)= l4-6iz-i-f bfz---b..., (12.47)

которую можно также получить, применив преобразование Лапласа к выражению (12.46) с последующей подстановкой е** = z

На г-плоскости функция К (z) имеет один полюс в точке г„ = Ь. Амплитудно-частотная характеристика рассматриваемого фильтра

К(е"")

- /(1)7"

I I -(co.s (1)Г - .sin шТ) I

1/1 . Ь\ -2h cos (,)Г

(12.48)

существенно зависит от знака весового коэффициента 6,. Форма АЧХ при нескольких значениях \bi\ показана на рис 12.17. При fej > О получается гребенчатый фильтр, выделяющий частоты ojT =- О, 2л.Т, 4л/Т, а при 6, <: О - частоты соГ л, Зл, 5л и т.д. С приближением \Ь\ к единице полоса прозрачности фильтра уменьшается, а усиление резко возрастает. Фазо-частотная характеристика рассматриваемого фильтра

( ((оГ) = - - arctg

b, sin ыТ 1 -Ii cos (О 7

(12.49)

Сопостави.м выражение (12.47) с (12.22). Видно, что (12.47) есть z-преобразование экспоненты, отвечающей условию е =г 6,. Следовательно, выражение (12.46) можно записать в форме

rr(t)= V е--««6(/-/Г) = е-« V b(t - kr

12.50)

Но это выражение есть не что иное, как результат дискретизации экспоненты е с шагом Т см. (2.122)1. Таким образом, приходим к заключению, что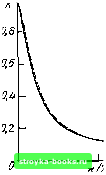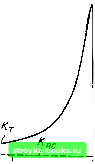

Зя/2

«7-

Рнс. 12.18. Амплитудно-частотные характеристики цифровой (сплошная линия) и ана-лоювой (штриховая) /?С-цепей при RC/T = S

дискретная импульсная характеристика gr (i) цепи, представленной на рис. 12.15, совпадает с последовательностью отсчетов импульсной характеристики g {t) аналоговой цепи (например /?С-цепи), постоянная времени которой 1/а = RC отвечает условию

e-« = 6i = e-/«c или /?С = Г/1п(1/&,).

При .этом, однако, АЧХ цепей существенно различны. Для дискретной цепи АЧХ определяется формулой (12.48). а для аналоговой С-цепи -выражением

У1 -h ((оУ?С)2 У 1 + (RC/T) (шТу

На рис. 12.18 АЧХ дискретной цепи (нормированная по максимальному значению) сравнивается с АЧХ аналоговой /?С-цепи при RC/T = 5 (чему соответствует 6, « 0,83). На участке 0<юТ<л обе кривые почти совпадают (при RC > 7"), а на участке л < u)T-< 2л ход АЧХ Кт обусловлен периодической структурой дискретного фильтра.

3. ТРАНСВЕРСАЛЬНЫЙ ФИЛЬТР ВТОРОГО ПОРЯДКА (рис. 12.19)

Разностное уравнение фильтра [см. (12.1)1 имеет вид Sbh.v (тТ) а„ S (тТ) + а, s (т - 1) Т) .s [(ш - 2) Г], а импульсная характеристика

gt (i) = Опб (/) + а,б (t-T)4-a&(t- 2Т). Передаточная функция в соответствии с (12.9) К(г) = ап 4 а, z --ат-- (ао?4 а, г-i-aa)/

Как и в предыдущих при.мерах, положим а„ = нули в точках

(12.51) Функция К (г) имеет

01 .02 -

Двухкратный полюс, расположенный в точке Zn = О, не влияет на поведение передаточной функции на г-плоскости.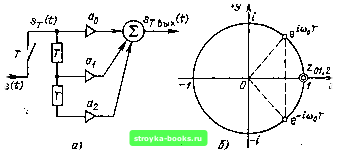

Рис. 12.19. Трансверсальный фильтр второго порядка (о) и положение нулей на г-плоскости (б)

Особый интерес представляет случай а„ == 1 и о, < 2, когда

01. (12 ---

Модуль этого выражения равен единице, так что комплексно-сопряженные нули Zo, и 2о2 лежат на окружности единичного радиуса (рис. 12.19,6).

Амплитудно-частотная характеристика подобного фильтра легко определяется из выражения (12.51) при подстановке а„ - \ я г- = е":

I К (е-П I -.= I 1 а, е- •• -f- е- (12.52)

Домножив правую часть этого выражения на le"*] = 1, получим АЧХ Iе"" -1-а, + е-" = 1 2 cosшТ + а, . (12.52)

Изменением коэффициента а, можно перемещать нули Zoi и z„2 по окружности единичного радиуса, что равносильно перемещению. нулей на оси частот.

В частности, при а, = -- 2 получается двухкратный нуль в точке 2=1. При этом АЧХ принимает следующий вид:

АЧХ 2cos мГ - Ij = 4 sin ((оГ/2).

(12.53)

2coso7--

График этой функции, представленный на рис. 12.20 сплошной линией, соответствует широко распространенному в практике режекторному фильтру второго порядка с бесконечно большим затуханием на частоте о)Т = О (е""= 1). /с

При а, = -]/Т нули z = {\/V2)x X (1 ± j) = e±"»", сорГ = 45° (см. рис. 12.19. б). Соответствующая АЧХ изображена на рис. 12.20 (штриховая линия).

Сопоставим выражение (12.52) в частном случае Oj = -2

I К (е-О I = М - 2е-""" + е-"

с аналогичным выражением (12.43) при а , - - 1

К(е"П = 1-е-"-].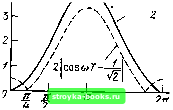

Рис. 12.20. Амплитудно-частотная характеристика фильтра (рис. 12.19, а) при ао=1, 02= 1 и ai = -2