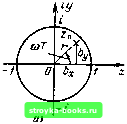Рис. 12.26. Положение полюса рис. 12.25

о ЫпТ

функции R (е"*) и АЧХ фильтра, показанного иа

График АЧХ при показанном на рис. 12.26, а положении полюса z, соответствующем сй>0, представлен на рис. 12.26, б. При изменении знака перед Ьд, т. е. при положении полюса ниже оси л;, полоса прозрачности фильтра будет в диапазоне со<: О или, что то же самое, в диапазоне л соТ 2я (на рис. 12.26, б АЧХ обозначена штриховой линией).

Итак, однополюсный резонатор, т. е. рекурсивный фильтр первого порядка с комплексным коэффициентом bj, позволяет осуществить фильтр, реагирующий либо только на положительную, либо только на отрицательную частоту. С понятием колебания отрицательной частоты как с физическим процессом мы встретимся в § 13.9 при рассмотрении квадратурной обработки сигнала.

Обратимся к рассмотрению цифрового трансверсального фильтра первого порядка с комплексным весовым коэффициентом.

В п. 1 § 12.8 было показано, что трансверсальный фильтр первого порядка (см. рис. 12.12) с действительным весовым коэффициентом а, позволяет осуществить режекцию (подавление) колебаний на частотах аТ = О и (оТ = 2л (при «1 = -1, см. рис. 12.14, б) или на частоте соТ = л (при а, = 1, см. рис. 12.13, б).

Найдем характеристики аналогичного фильтра при комплексном весовом коэффициенте а, == а,, -f iUy (рис. 12.27, а). Передаточная функция фильтра

K(2) = l-f о,г-1 (12.62)

имеет нуль в точке Zq - = а,, а разностное уравнение «вых(")= s(m) + aiSim - l).

Подставив s(m) = (m) -f is (m) и a, = -f ia„, придем к следующему результату:

«о вых (т) + is, „ь,х (т) = S, (т) -f а (т - 1) -s, (m - 1) + i [s, (m) -f + a .,.sjm~ l)-f 1).

Соответствующая этому алгоритму развернутая схема представлена на рис. 12.27, б.

Для определения АЧХ фильтра подставим в (12.62) z = е"" и а, = = а,. -1- iaij = - е""», где - частота, на которой должно обеспечиваться подавление колебания. Иными словами, нуль передаточной функции должен находиться на окружности \z\ - 1.

s(m)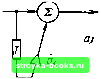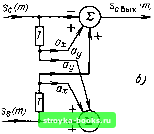

Рис. 12.27. Траисверсальный фильтр первого порядка с комплексным коэффициентом d(

Тогда

К(е»)= 1 е"оГе-«г 1 - cos (со - ©о) 7 sin (©-©о) Т и АЧХ фильтра

К(е)

Задавая весовые коэ(})фициенты соотношениями «д. = - cos ©п Т, а,, == = - sin ©оТ, можно перемещать нуль АЧХ во всем частотном диапазоне от О до 2д.

"г

12.10. ПРЕОБРАЗОВАНИЕ АНАЛОГ-ЦИФРА. ШУМЫ КВАНТОВАНИЯ

В предыдущих параграфах при изучении дискретных фильтров вопрос о неизбежной погрешности преобразования входного сигнала из аналоговой формы в цифровую не рассматривался. Погрешность возникает при квантовании сигнала на конечное, ограниченное число уровней. Чтобы выявить

характер этой погрешности, вернемся к структурной схеме на рис. 12.1 и выделим из нее два устройства: АЦП и ЦАП.

Рассмотрим сначала совместную работу этих устройств без учета цифрового фильтра при подаче на вход АЦП постоянного напряжения различного уровня «1 (рис. 12.28, а). Основным параметром АЦП является число разрядов, используемых для кодирования входного напряжения. При двоичном коде число разрядов определяется числом двоичных элементов (например, триггеров), каждый из которых может находиться в одном из двух состояний: с нулевым или ненулевым напряжением на выходе. Одному из этих состояний условно приписывается нуль, а другому - единица. При числе двоичных элементов г на выходе АЦП получается комбинация (кодовое число) из г символов, каждый

Рис. 12.28. Преобразование А-Ц и Ц-А (а), характеристика квантования (б) и ошибка квантования («)

из которых может принимать одно из двух значений (нуль или единица).

Как указывалось в §12.1, "число возможных различных комбинаций L = 2 и определяет число дискретных уровней, на которое может быть разбит диапазон изменения входного напряжения.

В ЦАП осуществляется обратное преобразование. Каждой комбинации нулей и единиц, поступающих на вход ЦАП, соответствует определенный дискретный уровень выходного напряжения. В результате при равномерном шаге квантования А зависимость и. от приобретает вид ломаной линии, показанной на рис. 12.28, б.

Устройство, представленное на рис. 12.28, а и обладающее подобной характеристикой, должно рассматриваться как нелинейное, а разность «2~ - Ui = q - как ошибка, погрешность квантования. Видно, что наибольшая ошибка, по абсолютной величине не превышающая А/2, с возрастанием «1 остается неизменной (рис. 12.28, в).

Продолжим это рассмотрение для гармонического входного колебания S (t) (рис. 12.29, а). Колебание Хцх (О приобретает ступенчатую форму, отличающуюся от входного колебания s (/) (на рис. 12.29, б, показанного тонкой линией), а ошибка квантования принимает вид функции

(0=«вык(0-5(0,

представленной на рис. 12.29, в.

При изменении в широких пределах амплитуды и частоты гармонического колебания s{t) изменяется только частота следования зубцов: форма их остается близкой к треугольной при неизменной амплитуде Д/2. Функцию q (t) можно назвать помехой или шумом квантования. Нетрудно вычислить среднюю мощность шума квантования. При допущении треугольной формы зубцов (рис. 12.29, в) с амплитудой А/2 средняя за длительность одного зубца мощность равна (1/3) (Д/2) Д712. Так как эта величина не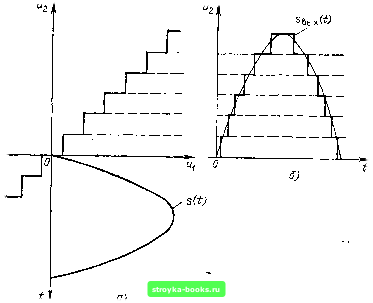

Рнс. 12.29. Сигнал на входе (а) и выходе (б) квантующего устройства; помеха квантования (в)