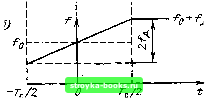
(13.27)

Таким образом, пик сжатого сигнала (в отсутствие усиления) выражен через корреляционную функцию исходного сигнала s (t). Применение выражения (13.26) иллюстрируется примерами, приведенными в следующем параграфе.

13.5. ПРИМЕРЫ ПОСТРОЕНИЯ СОГЛАСОВАННЫХ ФИЛЬТРОВ

1. ПРЯМОУГОЛЬНЫЙ ВИДЕОИМПУЛЬС

Зададим сигнал следующей функцией времени:

Е при 0<<Гс, О при < О и t>T,,.

Спектральная плотность такого сигнала, как известно,

S(co) £-1- (1 -e-с), S ((0): 2hincore/2 /со to

По формуле (13.8), в которой приравниваем длительности импульса Tf., находим передаточную функцию согласованного фильтра

К(1со)==£Л--(1 -е<-с)е-"с£Л -"" (13.29)

( - 1(0) /со

Рассматриваемый пример характерен тем, что К (ш) отличается от спектра сигнала S (ю) лишь постоянным коэффициентом. Ясно, что и импульсная характеристика фильтра g (t) совпадает по форме с самим сигнал01М s(t); действительно, из соотношения (13.15) следует, что

{ О при <0 и t>T.

График g {t)IA (рис. 13.6) по форме полностью совпадает с входным импульсом S (t).

Дальнейшая задача сводится к отысканию структуры физической цепи, обладающей импульсной характеристикой, изображенной на рис. 13.6, и передаточной функцией, определяемой формулой (13.29).

Простейший сигнал (13.27) удобен для иллюстрации основных положений синтеза четырехполюсника по заданной импульсной характеристике g (t) = = As (to - t) или, что то же, по комплексной передаточной функции К (щ), являющейся преобразованием Фурье от g (t).

Прежде всего отметим, что интеграл

f И"М dco = Г ((оГс/2)1-1п(о

J l+co J • "

Т. е. интеграл сходится, так что в рассматриваемом примере функция К (со) - AS (со) не противоречит критерию Пэли - Винера (13.16).

Показанную на рис. 13.7 структурную схему фильтра можно наметить непосредственно по передаточной функции (13.29). Входящий в эту функцию множитель 1/fco реализуется интегрирующим звеном, а второй множитель (I - е~"с) „ устройством вычитания, к которому сигнал попадает без задержки и с задержкой Т- Передаточная функция идеальной линии задержки (без потерь) равна е"""".

40.5

g(t)/A

tn/Z

Рис. 13.6. Импульсная характеристика фильтра, согласованного с прямоугольным импульсом

Рис. 13.7. Структурная схема фильтра, согласованного с прямоугольным импульсом

о 9i

Рис. 13.8. Формирование импульсной характеристики в идеальном (а) и физическом (б) фильтрах

Объяснить работу этой схемы можно также на основании временных представлений: при подаче на вход единичного импульса ЭДС [дельта-функции б {t)\ на выходе идеального интегратора появляется скачок напряжения в момент = 0. На выходе устройства получается напряжение в виде разности двух единичных скачков, сдвинутых относительно друг друга на время (рис. 13.8, а).

Реализация изображенного на рис. 13.7 устройства, которое обеспечивало бы точное интегрирование, а также задержку входного сигнала без искажения его формы (в пределах бесконечно широкого спектра единичного импульса), практически неосуществима. Можно, однако, получить достаточно хорошее приближение при использовании реальной интегрирующей /?С-цепи, если обеспечить постоянную времени этой цепи, достаточно большую по сравнению с Тд. При этом на выходе вычитающего устройства импульс напряжения, являющийся разностью двух экспонент (рис. 13.8, б), может быть реализован достаточно близким к прямоугольному.

Найдем напряжение на выходе фильтра. Применяя формулу (13.18) и учитывая, что корреляционная функция прямоугольного импульса имеет вид равнобедренного треугольника с основанием 27 и высотой, равной энергии импульса £Гд, получаем

8вых(0=ЛВЛ-д =

АЕ" t при О < < Те,

Л£(2Те-о при Ге<<2Те.

(13.31)

Максимальное значение выходного сигнала, равное Л£Тд, достигается в момент t == Тр, т. е. к концу действия входного сигнала (рис. 13.9).

Отношение сигнал-помеха в соответствии с (13.9)

5вых(П)/Овых = £КГс/0- (13.32)

Определим теперь пик сжатого сигнала по форму?1е (13.26). В данном примере В, (0) = £2 Г„ а

с с С

J В! (т) dt = 2 J BI (т) dx = 2 J £4 dT= 2£* -r„ 0 0

Следовательно,

г т„

П1/2

I Bl (т) dx

-]/3/2£.

Таким образом, вых (о)/- ==

Как будет видно из дальнейших примеров, пик выходного сигнала намного превышает амплитуду входного при согласованной фильтрации сложных сигналов (с большой базой).

2. РАДИОИМПУЛЬС С ЧАСТОТНО-МОДУЛИРОВАННЫМ ЗАПОЛНЕНИЕМ

Рассмотрим сигнал, изображенный на рис. 13.10, а. Огибающая этого сигнала имеет прямоугольную форму, а частота заполнения нарастает по линейному закону (рис. 13.10, б) со скоростью

р=.2(0д/П=2.2яуГе,

(13.33)

где - длительность импульса; 2(йд - полное изменение частоты внутри импульса; Юо ~ 2nfo - центральная частота заполнения. В дальнейшем исходим из условия, что 2(дд < cofl. Таким образом,

a>{t) = (Oo + f,t, -Tj2tTj2,

(13.34)

а мгновенное значение сигнала в интервале от -TJ2 до TJ2 определяется выражением

s(0-£ocos(c0o + pm).

(13.35)

Спектральная плотность подобного импульса была определена в гл.З. Было установлено, что модуль и фаза спектральной плотности определяются соответственно формулами (3.50) и (3.51).

Эти выражения могут быть в принципе положены в основу синтезирования фильтра, но создание четырехполюсника, точно реализующего столь сложные АЧХ и ФЧХ, представляет собой задачу трудную или даже вообще невыполнимую. Поэтому приходится прибегать к различным приемам аппроксимации АЧХ и ФЧХ. Первым этапом на этом пути является допущение о том, что огибающая спектра сигнала имеет прямоугольную форму, а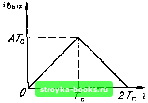

Рис. 13.9. Сигнал на выходе фильтра, согласованного с прямоугольным импульсом

Рис. 13.10. ЛЧМ импульс (а) и закон изменения мгновенной частоты (б)