13.6. ФОРМИРОВАНИЕ СИГНАЛА, СОПРЯЖЕННОГО С ЗАДАННЫМ ФИЛЬТРОМ

Рассмотрим одно интересное свойство схемы, представленной на рис. 13.17. На этой схеме Ki (ш) и Кг - передаточные функции фильтров на приемной и передающей сторонах канала связи, при этом выполняется условие

Ki (ICO) = к; (tco),

т. е. функции Ki (tw) и Кг («) являются комплексно-сопряженными.

При ударном возбуждении четырехполюсника Кг (t«) единичным импульсом б (О на его выходе возникает колебание (импульсная характеристика)

2(0 = j Кг (tco) е-dco,

которое используется в качестве сигнала, передаваемого по каналу связи. Таким образом, {t) s (t).

Нетрудно видеть, что по отношению к этому сигналу приемный фильтр Ki (ш) согласован, так как его импульсная характеристика gi (t) является зеркальным отражением сигнала s (t).

Действительно,

оо оо

g{t) = J- Г Kj (tco) е» dco = - Г К.; (tco) е» dco = 2п J 2я J

- оо - оо

= 2(-0=S(-0.

(Постоянная задержка t, входящая в выражение (13.15), здесь опущена.)

Сигнал «вых (О на выходе фильтра Ki (гсо) максимизирован в смысле соотношения (13.17).

Итак, для (юрмирования на передающей стороне сигнала, сопряженного с заданным приемным фильтром, можно применить принцип ударного возбуждения «обратного» фильтра. Под обратным подразумевается фильтр, передаточная функция которого комплексно сопряжена с передаточной функцией «прямого» фильтра.

Так как формирование сигналов и обработка в приемнике обычно осуществляются на промежуточной частоте, то схема (см. рис. 13.17) должна быть дополнена высокочастотным генератором и преобразователем для сдви-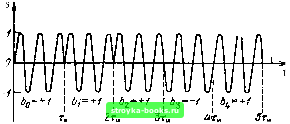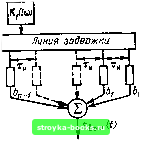

Рис. 13.18. Высокочастотное колебание, лированное по фазе

манипу-

Рис. 13.19. Структурная схема фильтра, согласованного с фазоманипу-лированным сигналом

4 14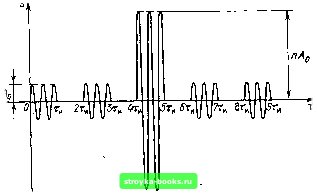

Рис. 13.20. Колебание на выходе сигналом

фильтра, согласованного с фазомаиипулированным

га спектра сигнала в область высокой частоты в передатчике, а также гетеродином с преобразователем для обратного преобразования частоты в приемнике.

Несмотря на кажущуюся простоту изложенного принципа формирования сигнала, обеспечивающего оптимальность его обработки в приемнике, реализация обратного фильтра является весьма сложной задачей, которая может быть успешно решена не для любого сигнала.

Относительно просто подобная задача решается для системы связи, в которой используется фазоманипулированный сигнал, представляющий собой последовательность радиоимпульсов, следующих без интервалов и различающихся между собой только фазой высокочастотного заполнения: начальная фаза в каждом из импульсов может быть либо О, либо я, причем чередование фаз осуществляется по определенному коду: fe-му импульсу приписывается коэффициент 6;,, равный ±1. Знак плюс соответствует фазе О, а знак минус - фазе п.

На рис. 13.18 изображен подобный сигнал из пяти радиоимпульсов с коэффициентами bQ - -j-\,bi = -i-\, Ь - -\,Ьз = - 1 и 64 = -Ь 1.

Структурная схема фильтра, используемого для обработки подобного сигнала, изображена на рис. 13.19, Фильтр представляет собой соокупность четырехполюсника К ((0)), согласованного с одиночным импульсом (с длительностью Тц), и многоотводной линии задержки. Число отводов, следующих через интервалы Тц, равно числу элементарных радиоимпульсов в сигнале. Безынерционные четырехполюсники Ь, Ь, Ь,... пропускают импульсы, поступающие с отводов линии задержки, без изменения или с изменением на 180° фазы высокочастотного заполнения импульсов.

Чередование коэффициентов Ь, Ь,... является зеркальным по отношению к сигналу. В результате напряжение на выходе приобретает вид, показанный на рнс. 13.20 (без учета влияния четырехполюсника Ki (iw) на форму импульсов).

К концу действия входного сигнала на выходе сумматора выделяется максимальный импульс с амплитудой пА„, где п - число элементарных импульсов. Таким образом, рассматриваемая цепь осуществляет сжатие сигнала, причем коэффициент сжатия равен п, т. е. числу отводов линии задержки. Число п в данном случае играет такую же роль, как произведение 2/дТс = т для фильтра, осуществляющего сжатие радиоимпульсов с частотно-модулированным заполнением.

Структурная схема обратного фильтра для получения сигнала, представленного на рис. 13.18, изображена на рис. 13.21. От схемы на рис. 13.19 эта схема отличается тем, что входной сигнал подается к противоположному концу линии задержки, благодаря чему чередование коэффициентов Ь, 61, *„ 1 является зеркальным по отношению к схеме рис. 13.19. Кроме того, передаточная функция четырехполюсника, осуществляющего внутриим-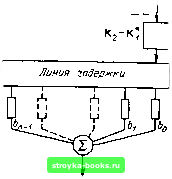

g(t)-s(f)

Рис. 13.21. Структурная схема фильтра, обратного по отношению к фильтру на рис. 13.19

пульсную обработку, является комплексно-сопряженной функции Ki (iw), обозначенной на рис. 13.19. Для импульса, симметричного относительно середины. Кг совпадает с Ki(iw). По существу, фильтры, показанные на рис. 13.19 и 13.21, совершенно идентичны, что является большим преимуществом, особенно в тех случаях, когда приемник и передатчик находятся в одном месте, например в радиолокаторе. В подобных случаях генерирование сигнала н его оптимальная обработка при приеме могут быть осуществлены с помощью одного фильтра. Подобная система получила называние ключ-замок.

13.7. ФИЛЬТРАЦИЯ ЗАДАННОГО СИГНАЛА ПРИ НЕБЕЛОМ ШУМЕ

Пусть на полностью известный сигнал s (t) линейно (аддитивно) накладывается шум с неравномерным энергетическим спектром W (со) (небелый шум). Требуется синтезировать фильтр, максимизирующий отношение сигнал-помеха. В отличие от ранее рассмотренных задач в данном случае передаточная функция должна б>1ть согласована не только со спектром сигнала S (со), но и с энергетическим спектром шума W (со) [22].

Наиболее простым способом отыскания требуемой передаточной функции К (ш) является приведение заданного шума к белому. Для выяснения сути этого способа рассмотрим вспомогательную структурную схему, показанную на рис. 13.22. На этой схеме К (ш) обозначает искомую передаточную функцию синтезируемого фильтра, а Ki (ш) и 1/Ki (ш) являются передаточными функциями двух вспомогательных условных четырехполюсников, введение которых не оказывает никакого влияния на работу устройства, так как их результирующая передаточная функция равна единице.

Так как функцию Ki (ш) можно выбирать произвольно, то модуль этой функции зададим в виде

Кг (а.)=К W„/W (со) , (13.49)

1де Wo - постоянная величина.

Тогда на выходе первого четырехполюсника будет действовать шум с равномерным энергетическим спектром

Wi (со) = W (со) IKi (cu)[2 = Wo = const, т. е. белый шум.

Само собой разумеется, сигнал на выходе этого четырехполюсника отличается от входного сигнала, так как спектральная плотность

S, (со) = S (со) К, (ш) (13.50)

отличается от 5 (со). Однако это обстоятельство несущественно; основной задачей является максимизация отношения сигнал-помеха на выходе всего устройства. Поэтому важно отношение энергии сигнала к энергетическому спектру шума, а форма сигнала при этом роли не играет.

Так как в рассматриваемом сечении схемы шум является белым, то для получения на выходе максимума отношения сигнал-помеха вся последующая часть устройства должна иметь передаточную функцию, отвечающую

условию (13.8). Таким образом.

К, (ш)

Рис. 13.22. Согласованная фильтрация заданного сигнала при небелом шуме

K(ia))=S; (w) е-»"».

(13.51)

Левая часть этого выражения является результирующей передаточной функцией четырехполюсника, обведенного на рис. 13.22 штри-