Следовательно,

где С - постоянный коэффициент. В момент t = О

(13.63)

- действительная величина, однако при tO Ва (f) является комплексной функцией:

B{t)=Bueit) + iBimit). (13.64)

Для выявления структуры согласованного фильтра воспользуемся соотношением вида (13.15) (постоянный коэффициент А заменен на С):

i{t)=CA*(tg-t).

Ограничимся здесь частным случаем симметричного сигнала [A{t)=A{-t)], а также опустим постоянную задержку to (обобщение см. в приложении 4). Тогда

g (t) = С А* (О = С [А (О cos е (t)-iA (t) sin в (01 -gRe (Л- iglm it),

(13.65)

где gRe (0 и im (t) - действительная и мнимая части комплексной импульсной характеристики согласованного фильтра g (t).

Сигнал на выходе фильтра определим с помощью интегральной свертки

5вых (0=1 S {Х) g (t - X) dx = Двух (t)-

(13.66)

Подставив в это выражение s (t) - (t) -f- iSg (t), a также импульсную характеристику no формуле (13.65), получим

00 оо

«ВЫХ (О = 5. «с (Х) gRe (t-x) dx+ S, (X) gim {t -X) dx -

- 00 -oo

oo oo "

\ So (X) glm (/ -X) dx-Ss (X) gRe (t -X) dx

i

-свых(0 + 5авых(0- (13-67)

Первый интеграл определяет отклик физической цепи с импульсной характеристикой (действительной) ge (t) на воздействие (О, второй интеграл

Sc(t)

Рис. 13.25. Согласованная фильтрация комплексного сигнала

- отклик цепи с импульсной характеристикой gim (О (также действительной) на воздействие (О и т. д.

Алгоритм (13.67) реализуется схемой, показанной на рис. 13.25.

Сопоставление выражений (13.64) и (13.67) показывает, что сигнал на выходе сумматора I соответствует функции СВре {t), а на выходе сумматора II - функции CBin, [t).

После дополнительной обработки (квадрирование и суммирование), по-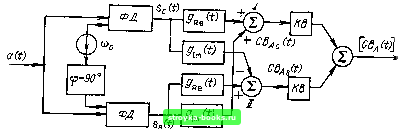

Рис. 13.26. Структурная схема согласованного фильтра

казанной в правой части полной структурной схемы (рис. 13.26), получаем окончательное выражение

[Sbmx (01 = С [Вас (t) + В% (t)] = С [Ва т (13.68)

Возведение в квадрат является нелинейным преобразованием. Однако эта часть обработки производится после максимизации отношения сигнал-помеха в линейной части устройства, поэтому взаимодействие сигнала и помехи проявляется незначительно.

Введем теперь в рассмотрение начальную фазу 9о, сохраняя прежние значения gRe (О и glm (О- Тогда функция А (х) под интегралом в (13.62) должна быть умножена на постоянное число е«, из чего следует, что при 9о О сигнал на выходе сумматоров I и II будет

СБа (О еб + sin % Вас т

U оудет

cos 00 Вас (О -sin Bas (t) + i [cos % Bac (t) +

a в результате последующей обработки на выходе всего устройства получится сигнал, совпадающий с выражением (13.68).

Таким образом, применение квадратурной обработки устраняет влияние неизвестной начальной фазы 9о на эффект фильтрации.

Итак, для осуществления согласованной фильтрации на видеочастоте в аналоговой форме требуется создание фильтров двух видов: с импульсными характеристиками (О - А (t) cos 9 (t) и дш (t) - Л (t) sin 9 (t).

При обработке сигналов сложной формы реализация указанных импульсных характеристик является трудной задачей. Например,при согласованной фильтрации ЛЧМ импульса эти характеристики должны быть следующими:

gne it) = COS pV2, gim (t) = sin f,t/2, \t\

Очевидно, что аналоговую обработку ЛЧМ импульсов затруднительно осуществлять с помощью квадратурной схемы в тракте видеочастоты. При цифровой же обработке отмеченные трудности устраняются.

13.10. цифровой согласованный ФИЛЬТР

Рассмотренные выше принципы квадратурной обработки, а также соотношения между сигналами на входе и выходе аналогового фильтра полностью распространяются и на цифровую обработку. Однако собственно

A(t)ccisS(t)

A-U.

A(t)sir\S(tJ

A-U,

Перемножитель

Л гт

ОбПФ

СВЛк)

К устройству исключения

Рис. 13.27. Согласованная фильтрация цифрового сигнала с использованием БПФ

фильтр обычно синтезируется на основе спектрального подхода, с использованием БПФ.

Поскольку согласованный фильтр должен выдавать на выходе сигнал, совпадающий по форме с корреляционной функцией входного сигнала, алгоритм фильтра можно построить по структурной схеме, представленной на рис. 13.27.

.На вход БПФ подается последовательность закодированных в цифру комплексных отсчетов {А (й)}, = 0,1, N - I, а последовательность спектральных коэффициентов {Za (л)}, п = 0,1, N - 1,с выхода БПФ поступает на набор перемножителей, осуществляющих умножение каждого из коэффициентов Za (п) на комплексно-сопряженный коэффициент Za (п). Полученная таким образом последовательность {Z (п) Р, п = О, 1, N - I, подвергается обратному быстрому преобразованию Фурье, и тем самым формируется последовательность отсчетов выходного сигнала \с точностью до постоянного коэффициента).

Последующая обработка по устранению влияния начальной фазы сигнала повторяет (в дискретной форме) обработку, показанную на рис. 13.26.

Сопоставление описанного цифрового согласованного фильтра с рассмотренными в § 13.5 аналоговыми фильтрами указывает на главное преимущество цифровой обработки - возможность реализации устройств с любыми импульсными и частотными характеристиками в пределах полосы частот, обеспечиваемой быстродействием преобразования А-Ц и арифметических устройств. Все сводится к выбору весовых коэффициентов. Факторы, характерные для аналоговых цепей: инерционность энергоемких элементов, влияние паразитных связей между отдельными узлами и их несогласованности и др., при цифровой обработке полностью отсутствуют. Важным преимуществом цифровых устройств является возможность расширения динамического диапазона увеличением разрядности АЦП (~ 6 дБ на один разряд, см. § 12.9).

Наконец, следует указать на высокую точность и стабильность характеристик цифровых фильтров, что особенно важно при сжатии сигналов с очень большой базой. Все эти преимущества достигаются ценой усложнения структуры фильтра, но, как показывает практика, современная микроэлектроника успешно справляется с возникающими в этой области проблемами.

Вместе с тем в ряде радиотехнических задач применение квадратурной обработки оказывается неприемлемым и болре предпочтительно осуществлять согласованную фильтрацию в тракте высокой частоты. Широко распространены аналоговые согласованные фильтры на линиях акустической поверхностной волны, на дисперсионных линиях задержки. Осваиваются новые способы, основанные на различных физических явлениях, таких, например, как спиновое эхо.