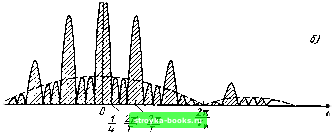Рис. 2.21. Модуль спектральной плотности пачки и.ч трех (о) и четырех (б) и.мпульсов

плотности пачки в N раз больше модуля спектра одиночного импульса. Это объясняется тем, что спектральные составляющие различных импульсов с указанными вьипе частотами складываются с фазовыми сдвигами, кратными 2л.

При частотах же со (1Л/) (2л Г), а также при некоторых других частотах, для которых сумма векторов е-* обращается в нуль, су.ммарная спектральная плотность равна нулю. При промежуточных значениях частот .модуль S ((!)) определяется как геометрическая сумма спектральных плотностей отдельных импульсов.

В качестве иллюстрации на рис. 2.21, а изображен спектр (модуль) пачки из трех прямоугольных импульсов, а на рис. 2.21, б - из четырех при интервале между соседними импульсами Т Зт„. Штриховыми линиями показана спектральная плотность одиночного импульса. С увеличением числа импульсов в пачке спектральная плотность все более расщемляется й в пределе при Л -* оо принимает линейчатую структуру спектра периодической функции (см. рис. 2.12).

2.1 I. БЕСКОНЕЧНО КОРОТКИЙ ИМПУЛЬС

С ЕДИНИЧНОЙ ПЛОЩАДЬЮ (ДЕЛЬТА-ФУНКЦИЯ)

Некоторые из возможных импульсов, площадь которых равна единице, изображены на рис. 2.22. Амплитуды всех этих импульсов обратно пропорциональны соответствующим образо.м определенной длительности. При стремлении длительности к нулю амплитуда обращается в бесконечность, а площадь импульса остается неизменной и равной единице.

Амплитуду прямоугольного импульса следует приравнять величине l/x, (рис. 2.22. а), где - длительность импульса.

при гауссовском импульсе (рис. 2.22, б) амплитуда должна быть приравнена \/]2ла. поскольку

е~-Г2ах = ] 2ла.

Наконец, для импульса вида sin (2я/т)/лх (рис. 2.22, в), площадь которого равна единице, амплитуда равна 2/ (при х = 0). Длительность импульса (главного лепестка) обратно пропорциональна параметру /„,.

При устремлении параметров х, и а к нулю, а к бесконечности все три изображенные на рис. 2.22 функции можно определить следующим образом:

g joo прих=0,

[О при хфО

при одновременном условии

j" S (х) dx = площадь импульса -I. (2.86)

Функция б (х), обладающая указанными свойствами, называется единичным импульсом, импульсной функцией или дельта-функцией (а также функцией Дирака).

Применительно к исходным функциям, изображенным на рис. 2.22, б и в, дельта-функция должна быть определена выражениями

б (л-) = lim-J-е~-/2", 6(x) = lim fsin (2л/„, х)яд:.

Возможны и другие многочисленные определения 6 (х). При сдвиге импульса по оси х на величину х„ определения (2.85), (2.86) должны быть записаны в более общей форме

б(х -х„) =

мри x = .v„.

•v,„

I О при V

\ 6 (X ,v„) dx -\,

6 (X - х„) = liin

6(x----x„) = Umt!llM-(£i:±i).

(2.87) (2.88) (2.89) (2.90)

о X.

-JL JL.

° S> в) f„

Рис. 2.22. Импульсы, обращающиеся в дельта-функцию при стремлении длительности

к НУЛЮ

функция б (х) обладает важными свойствами, благодаря которым она получила широкое распространение в математике, физике и технике. Из определений (2.87), (2.88) вытекает основное соотношение

тс, л:

\ 6{x-Xo)[(x)dx=,f(x„) \ b{x-x,)dxi(x„). (2.91)

Так как по определению функция 6 (х - х„) равна нулю на всей оси х, кроме точки X Хо (где она бесконечно велика), то про.межуток интегрирования можно сделать сколь угодно малым, лишь бы он включал в себя точку Хц. В этом промежутке функции / (х) принимает постоянное значение / (Хо), которое можно вынести за знак интеграла. Таким образом, умножение любой подынтегральной функции / (х) на б (х - х„) позволяет приравнять интеграл произведения значению / (х) в точке х х.

В математике соотношение (2.91) называется фильтрующим свойством дельта-функции.

В теории сигналов приходится иметь дело с дельта-функциями от аргументов t или О), в зависимости от того, в какой области рассматривается функция - во вре.меннбй или частотной.

Рассмотрим сначала свойства функции б (/). В этом случае основное значение имеет спектральная характеристика дельта-функции. В §2.10 было установлено, что при сокращении длительности т„ прямоугольного импульса (неизменной амплитуды) ширина основного лепестка спектральной плотности увеличивается, а величина 5 (0) быстро уменьшается. В данном же случае, когда уменьшение длительности импульса сопровождается одновременным увеличением его амплитуды, значение спектральной плотности остается неизменным и равным величине S (0) 1 для всех частот -оо < 0) <С оо. То же самое имеет .место при укорочении любого из импульсов, показанных на рис. 2.22.

Следовательно, спектральная плотность дельта-функции вещественна и равна единице для всех частот. Из этого также вытекает, что ФЧХ спектра дельта-функции б (t) равна нулю для всех частот. Это означает, что все гармонические составляющие единичного импульса при нулевых начальных фазах, суммируясь, образуют пик бесконечно большой величины в момент времени /= 0.

Аналогично функция б (/-о). определяющая единичный импульс в момент имеет спектральную плотность S (со)= е""*». Модуль этой функции по-прежнему равен единице, а ФЧХ 6 (си) - со/ц.

Найденная ранее спектральная плотность дельта-функции может быть получена и с помощью преобразования Фурье:

S(cu)= ( б(/ -/о)е-""Л.

- ос

Используя свойство (2.91), находим

S(о)) = е •» 1" б(/ - /о)с/ = е /2.92;

- оо

При t„ О S (со) = 1. Следует и.меть в виду, что правая часть равенства S (со) - 1 является размерной единицей: это площадь импульса, численно равная единице. Если под б (/) подразумевается импульс напряжения, то размерность S (oj) есть вольт X секунда (В-с).

На языке техники более подходящим по смыслу являлся бы термин стробирую-щее свойство.