
 |
|
Главная Цепи и сигналы [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [ 141 ] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] [167] [168] [169] для аппроксимации АЧХ различных фильтров. Этот вопрос рассматривается в гл. 15. 3. Полиномы Лагерра определяются формулой (14.12) Первые четыре полинома: Lo {х) = 1, Li (х) = -X + 1, La {х)=хУ2-2х + 1,1з (х>= -х/6 + + /iX-3x+l. Полиномы Лагерра ортогональны на полуоси О < л: < оо с весом р{х)= =. е-*. Так как полиномы Лагерра образуют систему расходящихся при х -ьоо функций, удобнее пользоваться функциями Лагерра (14.13) ;„=Кр(х)1Л)=е--/2 К{х). При этом функции Лагерра /„(х) ортогональны с единичным весом. На рис. 14.4 приведены функции Лагерра при п = 1,2,..., 5. Норма функции In (х) /п1 = /[/ {x)dx =1, поэтому при разложении функции / (х) по функциям Лагерра коэффициенты ряда / (X) = 2 " {X) должны определяться по формуле с„ - I / {X) и (х) dx. (14.14) (14.15) 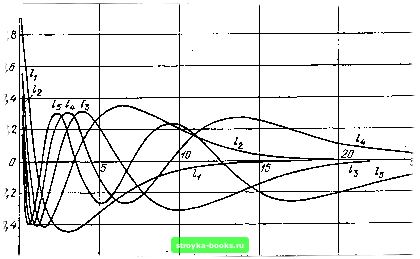 Рис. 14.4. Функции Лагерра (at) ус, с, Х7 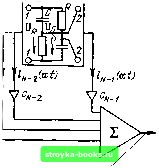 Рис. 14.5. Генератор функции Лагерра Функции Лагерра получили широкое распространение в измерительной технике и в многоканальных системах связи, что в значительной степени объясняется простотой их генерирования. Дело в том, что функция /„ (О по форме совпадает с импульсной характеристикой физической цепи, составленной из каскадного соединения простых звеньев (рис. 14.5). Для определения передаточной функции требуемой цепи применим преобразование Лапласа к функции Лагерра (14.13), предварительно заменив в (14.12), (14.13) переменную х новой переменной х = at: at/2 т In (at) =±-ЦП e-<t). Функции времени &-<H соответствует изображение л!/(р + а)"+1, а /г-кратному дифференцированию - умножение изображения на p. Учитывая также, что умножение на е«/2 дает сдвиг на р-плоскости на -а/2, приходим к следующему изображению для функции Лагерра: (Р-а/2)" р-а/2 \п (р + а/2)"+ (Р+а/2) I р--а/2 Передаточная функция первого звена \1(р + а/2) реализуется интегрирующей RC-тпъю, отвечающей условию RC = 2/а. Передаточная функция {р - а/2)/{р -Ь а/2) соответствует мостовой схеме при RC = 2/а. Действительно, непосредственно для мостовой схемы одного звена (см. рис. 14.5) , U2 2/Ui i =(Ur-~Uc)/Ui. i=(/? -l/ia)C)A/?-bl/i«C), откуда Us - 2 (Р)/и, 1 (/?) = (я -1 /RC)/(p + 1 /RC). При возбуждении цепи (см. рис. 14.5) дельта-функцией колебание на выходе первого звена будет е""°"/ = (а/), а на выходах последующих звеньев соответственно 1 (at), /а (at) и т. д. Взвешенное суммирование всех этих колебаний дает на выходе сумматора колебание / (at) Jy с„ /„ (at), t > О, где коэффициенты с„ определяются выражением (14.15). 4. Полиномы Эрмита определяются формулой (14.16) Первые пять полиномов Эрмита: Яо (jc) = 1, Я1 (х) = 2х, Hi ух) = 4x2-2, Яз (х) 8x - 12х, Я (х) = = 16х*-48x2+12. Графики этих полиномов представлены на рис. 14.6. Полиномы Эрмита ортогональны с весом р (х)= е--" на всей оси-оо< < X < оо, так что \ Я„(х)Я„(х)е--х- О при т Ф п, 2" У я п\ при т = п. Таким образом, норма функции Я„ (х) Yp {х) =Я„ (х) е- "1 Для перехода к ортонормированной системе полиномов Эрмита вводят функцию Фп {X) = Нп {x) Ур {x) Нп jx) е-/ \НпГр\\ У2"Уп (14.17) При этом разложение функции / (х) по нормированным функциям Эрмита записывается в форме /(х)= 2 СпФп(л), п = 0 Сп = j / (х) Ф„ (х) dx. (14.18) Графики нормированных функций ф„ (х) приведены на рис. 14.7. Из приведенного перечисления видно, что ортогональные системы функций можно разбить на два класса: I) системы, определенные на конечном интервале (полиномы Лежандра и Чебышева); 2) системы, определенные на бесконечном интервале, представляющем собой полуось О < X < оо (полиномы Лагерра) или всю ось - оо < X < оо (полиномы Эрмита). Для аппроксимации процессов и характеристик, определенных на конечном интервале, естествейно применять ортогональные системы первого класса. Для функций / (х), заданных в бесконечном интервале, целесообразно применять системы второго класса. При выборе полиномов важное значение - имеет вид весовой функции р (х), соответствую-- щей тому или иному виду полинома. Этот Рис. 14.6. Графики полино- ыбор должен быть тесно увязан с-харак-мов Эрмита тером аппроксимируемой функции f (х): ве- 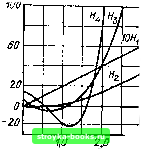 [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [ 141 ] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] [167] [168] [169] 0.0016 |