2. Спектр гармонического колебания s (t) = cos (ai + 9o) (рис. 14.17) в базисе функций Уолша. Как и в предыдущем примере, рассматривается один цикл гармонического колебания с периодом Т = 2я/со. Переходя к безразмерному времени О = t/T. записываем колебание s (t) в форме

Sj (6) = cos (2я6 + 9о) = cos9ocos 2я9 - sin Э, sin 2л9 = = Л cos 2я9 - B sin 2я9.

Спектр Уолша функции sin 2я9 определен в примере 1. Совершенно аналогично определение спектра функции cos 2я9 на интервале [0,1). Необходимо лишь функции sal (/, 9) заменить функциями cal (/, 9). Легко проверить, что при упорядочении по Уолшу новые коэффициенты Л, в ряде (14.27) будут Л(2), А (6), А (10) и А (14) вместо А (1), А (5), А (9) и А (13). При этом значения коэффициентов остаются прежними.

Таким образом, ряд (14.27) для рассматриваемого колебания можно записать в форме

Si (9) = cos 9о cos 2я9 - sin 9о sin 2я9 = cos 9о [А (2) wal (2 9) + +А (6)wal (6, 9)+(10)wal (10, 9)+Л (14) wal (14, 9)[ -sin9o [Л (1)х X wal (1,9)+Л (5) wal (5, 9) +Л (9) wal (9, 9) + Л (13) wal (13, 9)].

Итак, при сдвиге гармонического колебания по фазе спектр Уолша содержит четные и нечетные функции cal (/, 9) и sal (/, 9).

3. Спектр периодической последовательности прямоугольных импульсов (рис. 14.18) в базисе функций Уолша. Определим колебание s (t) на интервале [О, То) выражением s (t) - I, О < < т„, и соответственно

si(0) =

при О :

при о;

= т„/То.

(14.30)

Структура спектра Уолша заданного колебания сильно зависит от соотношения между т„ и Тд. Временная база То является дополнительным и произвольно выбираемым параметром функций Уолша. Действительно, при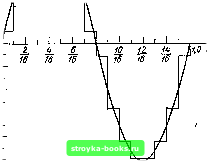

1,0 в

Рис. 14.17. Одни период гармонического колебания на интервале 06<1

®1

О П/То 1,0

Рис. 14.16. Аппроксимация синусоиды функциями Уолша

Рис. 14.18. Одни цикл периодической импульсной последовательности при т„/Г„=1/2

А 1.0

А 1/Z

J 1 L

0 11 го

А 1A

О 1 2 ш б)

{ I I

1 2 Ъ 4т

Рис. 14.19. Спектры последовательное прямоугольных импульсов в базисе функций Уолша:

а) при ти/Го=1; б) при ти/7")-1/2; в) при Ти/Го=1/4; =16

t:JTo - I спектр содержит лишь одну функцию wal (О, 0) с коэффициентом /4 (0) = 1. При rJTo - Va колебание (14.30) полностью определяется двумя функциями wal (О, 9) и wal (1, 9) с коэффициентами А (0) =Л (1) =/2.

Далее, при t:JTq ~ 1/4 использование формулы (14.28)

1 1 /4

А (w) = J" s (9) wal (w, Q)de= j wal (w, 9) dQ

дает следующие коэффициенты: Л (0) = Л (1) = Л (2) = Л (3) = 1/4.

Найденные спектры представлены на рис. 14.19. Этот результат легко обобщается для последовательности прямоугольных импульсов с отношением tJTg = 1/2*, где k - целое положительное число. Очевидно, что спектр Уолша такого колебания состоит из 2* компонентов с одинаковыми амплитудами, равными 1/2*. Очень важно, что этот спектр содержит конечное число составляющих; разложение того же колебания (14.30) по гармоническим функциям является бесконечным.

Рассмотрим теперь случай, когда т„/7о ф Va*, например, rJTg = Vg. Ограничиваясь первыми 16-ю функциями Уолша (в упорядочении Уолша) и опуская промежуточные выкладки, получаем Л (0) = Л (1) = = 1/3,- Л (4) =-Л (5) =Л (6) =Л (7) = %а, Л (8) = Л (9) = - Л (10) = = - Л (И) = - Л (13) = Л (14) = Л (15) = 1/24.

Найденный спектр представлен на рис. 14.20. При переходе к упорядочению по Пэли структура спектра сохраняется (по модулям).

Итак, при -Хи/ТоФ 1/2* спектр Уолша периодической последовательности прямоугольных импульсов содержит бесконечно большое число составляющих. Суммирование первых 16 функций дает импульс, показанный на рис. 14.21.

4. Влияние сдвига импульсной периодической последовательности на спектр Уолша. Рассмотрим этот вопрос на примере импульсной последо-

1/Нг

1/6 1/11 О

-1/11

/2тт

2 Y\6 8 ilii/f/J la

Рис. 14.20. Спектр последовательности прямоугольных импульсов в базисе функций Уолша при Гя/То=иЗ; N-\6

Ч. 0,5 в

Рис. 14.21. Аппроксимация прямоугольного импульса 16 функциями Уолша при Ти/Го=1/3, А=16

г 2

г г I ) t

о 2 6 & 10 12 /4- X

1 в

Рнс. 14.22. Одни цикл периодической последовательности импульсов на интервале 0,5<9<1

Щ А

hiliiaiiijiijji]

-L L

1,0 е

Рнс. 14.23. Влияние сдвига импульсной характеристики на спекур Уолша (ср. с рнс. 14.19, в)

Рнс. 14.24. Пример дискретных функций Уолша при iV=8

вательности при xJTg - (рис 14.22), смещенной на t„/2 относительно аналогичной последовательности (см. пример 3).

Используя функции Уолша (в упорядочении Уолша), определенные на интервале - Va 9 <; Va (см. рис. 14.11), запишем выражение для коэффициентов Уолша

А {w) = Г wal (w, 6) de,

откуда получаются следующие ненулевые коэффициенты: Л (0) = Л (2) = Л (4) = Л (6) = V.

Полученный спектр (рис. 14.23) вдвое шире спектра, представленного на рис. 14.19, в. Таким образом, сдвиг импульсной последовательности на вре-мт„/2 привел к изменению спектра. Зависимость структуры спектра от сдвиге? колебания S (t) на оси времени является особенностью анализа в базисе функций Уолша. Эта особенность связана с непериодичностью функций Уолша на единичном интервале их определения. Напомним, что при разложении по гармоническим функциям сдвиг сигнала во времени влияет лишь на ФЧХ спектра (см. § 2.7, п.1).

14.6. ДИСКРЕТНЫЕ ФУНКЦИИ УОЛША

Для цифровых методов спектрального анализа и обработки сигналов наибольший интерес представляют дискретные функции Уолша. Эти функции являются отсчетами непрерывных функций Уолша. Каждый отсчет расположен в середине связанного с ним элемента непрерывной функции. Длительность элемента равна \Ш от интервала [0,1).

В качестве примера на рис. 14.24 показаны первые две и последняя (Л - 1)-я дискретные функции Уолша при = 8. В качестве аргумента дискретной функции Уолша принят номер отсчета л: = 0,1..., Л- 1 (см. ось абсцисс на верхней части рис. 14.24). Основываясь на (14.21) и (14.22), можно получить общее выражение для дискретной функции Уолша

wal {w, х) = ( -1)

k= 1

(14.31)