области. В частности, диадная свертка двух временных последовательностей X (к) и у (k) записывается в форме

=jr 2 x{m)y{kem) = x{k)®y{k).

т= О

Основное преимущество ДПУ перед ДПФ заключается в том, что отсчеты сигнала умножаются на функции Уолша, которые принимают значения ±1 [см. (14.36), (14.37)1. По существу, операция умножения исключается и выражения (14.36), (14.37) сводятся к суммированию отсчетов с соответствующими знаками. В случае же ДПФ требуется умножение на комплексные числа вида е* N причем действительная и мнимая части этих чисел требуют представления достаточно большим числом разрядов (для снижения уровня шума округления).

По аналогии с БПФ и ОБПФ можно построить алгоритмы быстрых преобразований - прямого и обратного - по Уолшу.

Для вычисления N = 2 спектральных коэффициентов при использовании БПУ требуется всего Nr операций сложения и вычитания.

Возведение спектральных коэффициентов Уолша S (п) в квадрат и обратное преобразование Уолша дает диадную корреляционную функцию исходного сигнала. По своей форме эта функция сильно отличается от арифметической корреляционной функции. Кроме того, диадная корреляционная функция не инвариантна относительно положения обрабатываемого сигнала во времени. Эти обстоятельства препятствуют применению функций Уолша к такой, например, обработке сигналов, как согласованная фильтрация.

Тем не менее большое преимущество функций Уолша, не требующих использования операций умножения при обработке сигналов, способствует все большему их распространению в различных областях (передача изображений, распознавание образов, сжатие данных и др.)

Глава 15. ЭЛЕМЕНТЫ СИНТЕЗА ЛИНЕЙНЫХ РАДИОЦЕПЕЙ

15.1. ВВОДНЫЕ ЗАМЕЧАНИЯ

Общая теория синтеза линейных электрических цепей не входит в задачу курса «Радиотехнические цепи и сигналы».

В данной главе рассматриваются лишь некоторые частные, специфические для синтеза радиоцепей вопросы:

синтез активных четырехполюсников в виде каскадного соединения элементарных невзаимодействующих (развязанных) звеньев первого или вто-рого\порядка;

построение избирательных цепей, не содержащих катушек индуктивности (интегральные микросхемы);

элементы синтеза дискретных (цифровых) цепей и соотношение между АЧХ и ФЧХ цифровых фильтров.

Синтез аналоговых цепей в данной главе проводится лишь в частотной области, т. е. по заданной передаточной функции; для цифровых цепей рассмотрен синтез и по заданной импульсной характеристике (кратко).

Известно, что передаточная функция линейного четырехполюсника однозначно определяется своими нулями и полюсами на /7-плоскости (аналоговые цепи) или на z -плоскости (цифровые цепи). Поэтому выражение «синтез по заданной передаточной функции» эквивалентно выражению «синтез по заданным нулям и полюсам передаточной функции». Существующая теория синтеза четырехполюсников рассматривает цепи, передаточная функция которых имеет конечное число нулей и полюсов, иными словами, цепи, состоящие из конечного числа звеньев с сосредоточенными параметрами. Излагаемый ниже материал ориентирован на четырехполюсники с небольшим числом звеньев, которые характерны для фильтров нижних частот, верхних частот, заградительных фильтров и т. д., широко применяемых в радиоэлектронных устройствах.

15.2. ПРЕДСТАВЛЕНИЕ АНАЛОГОВОГО ЧЕТЫРЕХПОЛЮСНИКА КАСКАДНЫМ СОЕДИНЕНИЕМ ЭЛЕМЕНТАРНЫХ ЧЕТЫРЕХПОЛЮСНИКОВ

При заданных нулях и полюсах передаточную функцию К {р) целесообразно представлять в виде произведения множителей, каждый из которых может являться передаточной функцией простейшего, элементарного четырехполюсника. Пусть, например, передаточная функция синтезируемого четырехполюсника

К(р) = -22--- (15.1)

Ьй (Р - Рт)(Р - Рпг) (Р - Рпз)

обладает нулем в точке р = О и тремя полюсами, из которых один вещественный в точке pjti < О и два комплексных: pi Рпз = Рп2-Учитывая равенство

(р -pJ (р -р1,) = -2 Re ip,) р +1 р„а \\ (15.2)

записываем (15.1) в форме

V,(p) = ----!-=-Ki(p)K2(p). (15.3)

Передаточная функция Ki (р) реализуется звеном первого порядка {RC-или/L-цепь). Действительно, для/?С-цепи (рис. 15.1, а) при съеме напряжения с резистора передаточная функция

Ki(p)= =--, (15.4)

откуда следует pi = -1/RC, /?C=1/Pni. При использовании RL-цет (рис. 15,1, б)

Ki(p)= =-(15.5)

откуда = -R/L.

Функция К2 (р) реализуется звеном второго порядка.

Трактовка выражения (15.3) как передаточной функции каскадного соединения взаимно независимых четырехполюсников Ki (р) и Кг (р) позволяет задачу синтеза сложного четырехполюсника свести к синтезу простых звеньев. Увеличение числа нулей и полюсов в передаточной функции приводит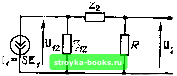

Рис. 15.1. Примеры четырехполюсника первого порядка

Рис. 15.2. Реализация типового звена второго порядка

лишь к соответствующему увеличению числа звеньев. Естественно, такой подход имеет смысл и допустим лишь при достаточной развязке элементарных четырехполюсников. Применение эмиттерных повторителей и некоторых других устройств современной микроэлектронной техники обеспечивает выполнение этого требования. В тех случаях, когда нельзя пренебрегать взаимным влиянием элементарных четырехполюсников, приходится прибегать к более сложным методам синтеза, излагаемым в специальной литературе.

Передаточную функцию элементарного четырехполюсника второго порядка в соответствии с (15.3) зададим в форме

К(/)-ао

(15.6)

где постоянные коэффициенты 6i = - 2 Re (рп), = ЬпР. &о = 1-

Рассмотрим сначала реализацию функции К {р) с помощью цепи, содержащей катушку индуктивности L, конденсатор С и резистор R (рис. 15.2). Сопротивление резистора, являющегося нагрузкой четырехполюсника, считаем заданным. Один из элементов цепи Zg, должен быть индуктивным, а другой - емкостным. Под источником тока, возбуждающим цепь, можно подразумевать, например, коллекторную цепь транзисторного усилителя, работающего по схеме с ОЭ (см. рис. 5.8, а). Внутренней проводимостью источника тока пренебрегаем. Ток равен SEi, где Ei - напряжение база- эмиттер.

Напряжение на элементе Z можно определить выражением

Ul2 = 12 (2 + R) 5Ei/(Zi2 + Za + R),

a напряжение на резисторе R - выражением R R (Zj + R)

R + Z, Следовательно, и.

Ul2==

Kip) = - = S-

E, Z, + Zi + R

(R+Z) (Z,i+Zi + R)

SE,.

(15.7)

Из сопоставления этого выражения с (15.6) очевидно, что для получения вещественного числителя следует задать = 1/Ср hZo = Lp. При этом

1 SR 1

K(p) = S/?

+ LP + R

(15.8)

Сравнение (15.8) с (15.6) приводит к равенствам R/L = Ь,, \ILC= == SRILC - ао, откуда

L = Rlb; С == MbL; = SRb.

(15.9)