
 |
|
Главная Цепи и сигналы [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [ 152 ] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] [167] [168] [169] Как и передаточная функция Кг (г) [или К (е"" )1, логарифмическое затухание Ат (ю) и ФЧХ дискретной цепи являются периодическими функциями частоты. Это позволяет существенно упростить соотношения, связывающие между собой АЧХ и ФЧХ. С этой целью запишем функции Ат{(й) и фт(о)) в виде рядов Фурье: Л7 И = 1п IК (е - •) I Ло + Л1 cos шТ + Л-з cos 2(оТ + ..., (15.56) ф7•((o)==ФlSiпcor + Ф2siп 2аТ + ... (15.57) Косинусоидальный ряд для Ат (ю) обусловлен четностью этой функции относительно ю, а синусоидальный ряд - нечетностью функции фг (ю). Соответственно коэффициенты рядов (15.56) и (15.57) определяются формул ами л„=- - я я Фп = Лг(ю) COS пюТй(юТ), (15.58) J„ = J ф7(ю)51пп(оГй((оГ). (15.59) Подставим ряд (15.56) в (15.55): (ы) =А« г ctg [((О -(Oi) Т/2] d{(oT) + Г cos (оГ X 2я J 2я J - я -я Xctg[(co-coi)T/21d((Dr)+ J cos2(or-ctg[((u-cDi)T/2]d((oT)-b... Первый интеграл равен нулю, а последующие 2п (- sin пщ Т). Таким образом, приходим к следующему ряду для фг (соО (опуская индекс 1 при О)): Ф7-(ш)=.- V Л51птоГ. (15.60) п== 1 Аналогично подстановка ряда (15.57) в (15.54) приводит к выражению Лг(ю) = Ло- 2nCosnaj7. (15.61) /1= 1 Из сопоставления рядов (15.60) и (15.57),а также (15.61) и (15.56) вытекает важное соотношение Л„--Ф„. (15.62) Следовательно, по заданной функции Ат (ю), записанной в виде ряда Фурье, можно найти коэффициенты Ф„ ФЧХ фг (ю). При заданной ФЧХ (также в виде ряда Фурье) функцию Ат (ад) можно найти с точностью лишь до Ло. Физический смысл этого факта очевиден, так как величина Ло Г 1пК((й)Й(йГ, 2зх зависящая только от АЧХ фильтра К («), может изменяться в широких пределах (изменением усиления) при сохранении ФЧХ.
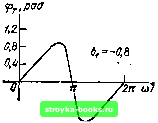 Рис. 15.14. Фазо-частотиая характеристика цифрового фильтра, соответствующая АЧХ, равной 4sin2 (й)Г/2) Рис. 15.15. Фазо-частотная характеристика цифрового фильтра с АЧХ, равной l/l/l-fbf -26j coswr Итак, ДЛЯ полного описания передаточной функции минимально-фазовой цифровой цепи достаточно знать коэффициенты Фурье одной из характеристик: ФЧХ Фг(«) или логарифмического затухания Ат (со). Вычисление коэффициентов ряда Фурье любой из характеристик Ат (со) и срт- (со), заданной на интервале О < соГ < 2п, несравненно проще, чем вычисление интегралов в бесконечных пределах, требующееся при анализе аналоговых цепей [см. (15.49) и (15.50)[. 15.10. ПРИМЕРЫ ОПРЕДЕЛЕНИЯ ФЧХ ЦИФРОВОГО ФИЛЬТРА ПО ЗАДАННОЙ АЧХ 1. Задана АЧХ фильтра Су. (шГ) - 4 sin (шГ/2), - я < мГ < я (см. п. 3 § 12.8). Требуется найти ФЧХ (не выясняя схемы фильтра). В данном примере логарифмическое затухание Aj (м) = 1п Кт (шГ) = 1п44-2 1п81п(шГ/2), -л<(оГ<л. Находим коэффициенты Фурье периодической функции Aj (со) по формуле (15.58) 1: (0)Г)=г1п4 + - J \п (s\n х) d (2х) =Q, \пА-\-2 In 1п 4 + 2 1п (О Г cos п(.йТ(1 ((ОГ) = -- . Итак, Ло = О, = - 2-1, А-= - 2-Ч,,Аз - - 2 1, ... Основываясь на выражении (15.60) составим выражение для ФЧХ фильтра Фт- ((й) = 2 (sin соГ + 1/2 «!п2соГ + 1/з sin ЗшГ+ ...), -л <а)Г <л. Полученный ряд сходится к (я - со Г)/2 при О < w Г < 2я, следовательно Фт-(со)=я-соГ, 0<шГ< 2л. График 9j. (w) представлен на рис. 15.14. Продолжение в область шТ < О (штриховая линия) основано на периодичности функции фу. (со). Заметим, что полученная характеристика совпадает по форме с ФЧХ однозвенного фильтра, рассмотренного в п. 1 § 12.8. Каскадное соединение двух звеньев, соответствующее АЧХ, равной 4 sin о)Г/2, приводит лишь к удвоению ФЧХ. 2. Рассмотрим теперь фильтр с АЧХ (см. п. 2 § 12.8) Kj (соГ) ~1/У I + Ь\ -26i cos (О Г . См. [31], формулы (4.224.3) и (4.384.3). Логарифмическое затухание Aj. ((i))eln Kf (ы) =--- in (1-26i cos mT+bl). Находим коэффициенты Фурье я An-- ( - 1/2) In (1-26i cos ыГ + &?) cos nrnTd (шГ). Выполнив интегрированые i, получим Таким образом, (w) = -У - sin пшТ. Используя соотношение 1"} 6i sin x - sin лд; = arctg --- rt= 1 cos X получаем выражение, совпадающее с (12.49): bl sin соГ (pj (co) = -arctg • 1-6i cos шГ , -я<шТ<я. График ФЧХ для bl = 0,8 представлен на рис. 15.15 (иа интервале О < соГ < < 2я). 3. Задан цифровой ФНЧ с АЧХ, приближенно совпадающей с гауссовской кривой: 1к(е""01~е- (*>г>. Найти ФЧХ фильтра. В данном примере Aj. (w) = lnl!?(e") = -я2 (соГ)2. Вычисление коэффициентов An по формуле (15.58) дает следующие результаты: Л„=----а\ Ai=4a\ А-а, -3=- Таким образом, Фт- (со) = - 2 sin/icoT = п=! -4 sin wT-f sin 2шГ --sin ЗшГ-f -f - sin 4шГ - sin SwT-f ... Графики Фт- (to) для двух значений параметра а показаны на рис. 15.16. 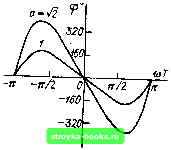 1 См. [31], формула (4.397.6). 2 См. [31], формула (1.448.1). Рис. 15.16. Фазо-частотная характеристика цифрового фильтра с АЧХ, равной ехр [-а{(оТ)Ц [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [ 152 ] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] [167] [168] [169] 0.0013 |
||||||||