(Re S(n)} Jq у

{Im5(n)}

Рис. 16.11. Определение, кепстра мощности свернутого сигнала (цифрового)

Переходя к модулям S = [Re S (п)] + [Im S (п)] и логарифмируя, получаем чисел вида In 1 S (п) . Применив, наконец, ОДПФ

C,{m)=-L 2 lnlS(rt)e m = 0, 1, 2N - 1,

(16.22)

п = 0

найдем кепстр мощности сигналов.

Алгоритм перечисленных выше преобразований представлен на рис. 16.11.

Вычисление кепстра мощности дискретного сигнала будет рассмотрено в следующем параграфе.

16.6. ОПРЕДЕЛЕНИЕ ЗАДЕРЖКИ СИГНАЛА

В ряде областей техники приходится иметь дело с обработкой сигналов, являющихся суммой исходного (зондирующего) сигнала и сигнала, отраженного от различных объектов. К таким областям относятся радиолокация, сейсмология, акустика и др. Сигнал на входе устройства обработки можно представить в форме

S (т) = Si (m) -}- а Si (m - т.), а <; 1, (16.23)

где {Si (m)}, m==0,l,..., N - 1, - дискретизованный зондирующий сигнал, представляющий собой эквидистантную последовательность отсчетов с шагом Т; а (т - т) - отраженный сигнал, который можно трактовать как задержанную на время - тТ копию исходного сигнала.

Пусть исходному сигналу {si (m)} соответствует z -преобразование Si (z).

Тогда г-преобразование последовательности as, (т - Шд) будет aSi (г)г-«», а суммарного сигнала {s (т)}.

8(г)= Si (г) + а Si (г) г-

:5цг)(1+аг-".)=: Si(2)s2(2).

(16.24)

Из (16.24) следует, что определяемый выражением (16.23) сигнал s (m) можно трактовать как свертку s (m) = Si (m) (g) (m), где Sj (tn) - сигнал,

г-преобразование которого равно 1 + az-""-Таким сигналом является сумма двух дельта-функций (рис. 16.12):

Si (0 = б(0 + аб (t-moT).

Это обстоятельство имеет фундаментальное значение, так как показывает, что широкий класс задач в перечисленных ранее областях, в которых приходится иметь дело с отраженными сигналами, сводится к обработке свернутых сигналов.

Рис. 16.12. +аб(/-тоГ)

Сигнал б(/) +

Существенно, что множитель (г) = (1 + аг-"»») в выражении (16.24), учитывающий задержку отраженного сигнала тТ и коэффициент отражения а, от структуры спектра исходного сигнала не зависят.

Обратимся к (16.24) и, учитывая, что контур интегрирования в (16.20) совпадает с окружностью единичного радиуса на г -плоскости, подставим в множитель (1 + аг-"") вместо г переменную е<".

Тогда

1 2 (е") Г = I 1 + а е-»"« = (1 + а е - 0(1+» е«"" ) =

= 1 4-а2+2асо.5(а)тоГ). (16.25)

Таким образом, выражение (16.24) позволяет составить следующее соотношение:

5(еа)Г = ISj (е") Г(1 f а= + 2асо5((о/ПоГ)!. (16.26)

Из (16.26) видно, что наложение задержанной копии ccSj {т - т) на

исходный сигнал Sj {т) создает эффект модуляции спектра энергии Si (е<") р по закону 1 + + 2а cos (ы/Пц Т). Глубина модуляции определяется коэффициентом 2а/(1 + а=), а период модуляции равен 2л По.

С аналогичным явлением мы встретились в примере предыдущего параграфа, где спектр энергии исходного сигнала также являлся периодической функцией (0.

Прологарифмировав выражение (16.26), получим

1п 1 S (е") Р = 1п I Si (е"0 1 + 1п [ 1 + а + 2а cos (сошо Т)].

(16.27)

Примерный вид слагаемых правой части показан на рис. 16.13. Вычислим кепстр мощности по выражению (16.20), которое на основании (16.25) -(16.27) можно записать в форме

с, и = J 1п I S; (е"0 Г COS (та)Г) d (шГ) + ±- j 1п 1 +

+ ае

- «Шо (лТ I

COS (тслТ) d(aT)= C,i (т) -f- С,2 (т).

(16.28)

Как видно, информация о задержке содержится в кепстре Сз (т), поэтому вычисление начнем именно с Сз (т), не уточняя пока структуры сигнала Si (т) и кепстра (т).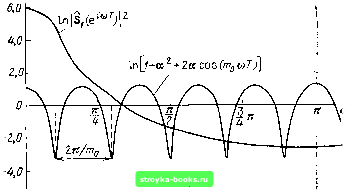

Рис. 16.13. К выражению (16.27); а = 0,8, то=10

Основываясь на выражении (16.25), получаем

1п1 1+ае-""«-Р=1п(1 +ае-""»<-0 + 1п(1 +а е»"» <").

Так как ае-"» (< 1, можно воспользоваться разложением

ln(l+x)=x -xV2 + x«/3 -...

Тогда

In I 1 + а е- "» р = а (е-"»+ е"" "О - (е- 2"" + е"» "О +

+ - (е-3". + е3«« »г) -... = 2а cos {т юГ) -cos (2mo ыГ) + 3

+ - 2 cos (3/По(вГ)-...

Подставив этот результат во второе слагаемое в правой части (16.28), п олучим

С,2 (/п) = а I - Г cos [(т- тц) соГ] d (соГ) + - Г cos [(m + т) юГ] X

. - л - л

X й (соГ)! - Г COS [(/п- 2/По) ыГ] d (соГ) +

?л J

COS [(т+2/По) соТ] d (соТ) + ...

Очевидно, что С, (т) отлично от нуля только в точках т = + т, m = ± 2 /По и т. д., причем

C,2(mo) = C,2(-mo)=a, С,2(2то)-С,2(-2/По) =-а2, С,2(Зто) = = С,2(-3/п„)=аЗ/3, ...

Кепстр (т) представлен на рис. 16.14. Истинная задержка определяется по положению первого пика.

Найденный выше кепстр Cs (т) наблюдается на фоне кепстра Ci (т) исходного сигнала. Для надежного определения /о требуется достаточное превышение Cs2 {tn) над Ci (т), а также разнесение их на оси кепстрального времени тТ. Важно, чтобы кепстр Csi (т) концентрировался вблизи начала отсчета кепстрального времени. Кроме того, кепстр Csi (т) должен быть свободен от ложных пиков. Степень выполнения этих требований зависит от структуры спектра (со) исходного сигнала Sj (t). Некоторые соображения по этому вопросу приводятся в следующем параграфе.

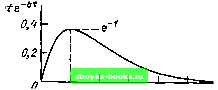Рис. 16.14. Кепстр Cs2(m) при а=0,8 482

20 40 00 80 100 т=т/Т

Рис. 16.15. Сигнал Si{t)=At->\ нормированный к величине Л/6, 6Г=0,05