IfMnynbC sayccodcmu h- ---

0,b 0,6

Прямоуаольный * Треуаольный d)

0,5 1,0 i,5 f r-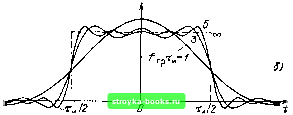

Piic. 2.23. Доля энергии сигнала в полосе /грТ,, (а) и деформация импульса при усечении спектра (б)

q)t„/4

dco=3r] (сй,р т„/4),

где т1(со,рТ„/4)=т1

sin* л:

Для гауссовского импульса в соответствии с (2.77) получаем

гр "~"гр

о "0

где 5 = Ла - полная энергия гауссовского импульса, а функция 2 Г

Ti(acOpp)=-- е-"dx (ao:).)-интеграл вероятности. Ул J

Учитывая, что длительность гауссовского импульса определена в п. 3 §2.10 и равна 2а, аргумент функции г можно записать в форме асор = = я/грТ„. Функции т] для трех импульсов представлены на рис. 2.23, а.

Итак, значение произведения /грТ„, требующееся для заданного т], максимально для прямоугольного импульса (при т) > 0,9) и минимально для гауссовского. В частности, уровню т] = 0,95 соответствуют значения /,рт„, равные 1,8; 0,94 и 0,48.

Выбор границы спектра по энергетическому критерию в некоторых практических задачах не всегда приемлем. Так, если при обработке импульса требуется сохранить его форму достаточно близкой к прямоугольной, то /грТи должно быть гораздо больше единицы. Для иллюстрации этого важного положения на рис. 2.23, б показаны исходный импульс (штриховая линия) и его деформация при усечении спектра на уровнях /рТ,, = 1,3 и 5.

В любом случае при заданной форме сигнала сжатие его во времени с целью, например, повышения точности определения момента его появления

1 Последовательное интегрирование по частям приводит к следующей формуле: b

fsin x 1

--dx = - x* 3

Ф (fe)

Ф" (Ь)

-2si (26)+4 si (46)

где ф (6) = sin* 6; ф(6) = - (2 sin 26 -sin 46); ф" (6) =26 (cos 2-cos 46).

неизбежно сопровождается расширением спектра, что заставляет расширять полосу пропускания измерительного устройства. Аналогично сжатие спектра импульса с целью повышения точности измерения частоты неизбежно сопровождается растяжением сигнала во времени, что требует удлинения времени наблюдения (измерения). Невозможность одновременно сконцентрировать сигнал в узкой полосе частот и в коротком интервале времени представляет собой одно из проявлений известного в физике принципа неопределенности.

Вопрос о величине произведения длительность X полоса актуален в связи с проблемой электромагнитной совместимости, возникающ,ей при взаимных помехах радиостанций. С этой точки зрения наиболее желательна форма импульсов, близкая к колоколообразной.

2. СКОРОСТЬ УБЫВАНИЯ СПЕКТРА ВНЕ ОСНОВНОЙ ПОЛОСЫ

Для выявления связи между поведением S (со) в области относительно высоких частот и структурой сигнала s (t) воспользуемся свойствами таких испытательных сигналов, как единичный импульс и единичный скачок.

Единичный нмпульс б (/) является единственной функцией, имеющей неубывающую спектральную плотность на всей оси частот - оо <; со < оо.

Поэтому можно утверждать, что сигнал s (/), спектр которого вне основной полосы не убывает с ростом со, содержит в своем составе дельта-функцию (в реальных условиях достаточно мощный короткий импульс).

Далее, единственной функцией времени, имеющей спектральную плотность вида 1/со, является единичный скачок и (t) ~ I, t 0. Следовательно, убывание хвоста спектра сигнала s (i) по закону 1/со свидетельствует о наличии в функции S (t) скачков, т. е. разрывов непрерывности. Но в точках разрыва производная функции обращается в дельта-функцию (с постоянны.м коэ({)фициентом, равным величине скачка). Поэтому убывание спектра пропорционально 1/со указывает на наличие дельта-функции в составе производной s (t). Это рассуждение можно продолжить и для производных сигнала S (t) более высоких порядков.

Проиллюстрируем сказанное примерами трех сигналов, представленных на рис. 2.24: с разрывом, с изломом и «гладкого» сигнала (без разрывов и изломов).

В первом примере (рис. 2.24, а) производная s (t) определяется выражением

s(0 = 6(0 -ае-«, fO, а = 1/Го,

и спектральная плотность функции s (t) в соответствии с табл. 2.1

(со) = 1 -ОС -L -.

а + (й) а + г (ш)

Для определения спектральной плотности сигнала s (t), являющегося интегралом от s (t), можно исходить из выражения

S,(co) =-Ls,.(co) = - .

В данном случае операция I/ico законна, поскольку Ss (0) = О [см. (2.60)].

При со > а спектральная плотность (ci)) 1/гсо. Как видно из рис. 2.24. а, это объясняется наличием функции б (t) в первой производной сигнала s (t).

g Таблица 2.1

Сигнал

Изображение по Лапласу

Спектральная плотность

1 при i Sj О, О при /< О,

яб (ш) +- ш

S (О-

при / > О, при / < О

а > О

-яг/2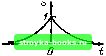

S (0=е-«11, а> О

«2 + 0)2