оо - oo

Кепстр рассматриваемого сигнала s{t) содержит всего лишь один импульс б {q- - to), задержанный (на оси q) на время Iq.

Приведем еще пример континуального сигнала вида

s{i) - \/nt, -оо < < оо ,

для которого спектральная плотность

S(.)=J

г оо

COSM/ , с sin со/ --dt-i I ---dt

= -i при О) > о, = +( при й)< О

(см. § 3.9, с. 93).

Учитывая, 4T0=F( = и In (е""/) = + inl2, получаем

- 1л/2 при О) > О, + (я/2 при ш <0.

In S (со) =

Таким образом. In S (со) отличается от S (со) только коэффициентом я/2 из чего следует, что кепстр рассматриваемого сигнала s (/) = 1/я/

В данном примере кепстральное преобразование не изменяет формы функции. Приведем еще пример сигнала вида

s(t) = а In (а2 + t),

для которого спектральная плотность S (со) = е~"°*1 и In S (со) = - асо. Запишем это выражение в следующей эквивалентной форме:

-а (- i) (/со) при (О > О,

-а ( + 1) ((со) при со < 0.

От предыдущего примера In S (со) отличается множителем /со, соответствующим операции дифференцирования, а также заменой л/2 на а; следовательно, обратное преобразование Фурье, определяющее кепстр, дает

In S (со) =

d I \ а

16.10. СВОЙСТВА КОМПЛЕКСНОГО КЕПСТРА

Одной из основных операций при определении кепстра является логарифмирование спектральной плотности входного сигнала. Рассмотрим этот вопрос сначала с позиции континуального сигнала s {t), спектральная плотность которого S (со) = S (со) e"®s .

Логарифм этой функции следует записывать в общей форме

In S (со) = In S (со) + iB, (со) = In S (со) + / [9, ,„ (со) + к2я]. (16.45

Предполагается, что ФЧХ спектра (со) - непрерывная антисиммет -ричная функция со, а Эл (м) - главное значение аргумента, определяемое «по модулю 2л», т. е. с отбрасыванием целого числа 2л, так что [бгл •

Неоднозначность можно устранить, основываясь на непрерывности функции 6s (со) и задании ее значения на какой-либо фиксированной частоте.

Из-за нечетности функции 9 (со) целесообразно положить 9 (0)==0

Продис})ференцируем 1п S (со) по частоте:

l lnS(co)=-i- . (16.46)

dco S (со) dco

Тогда функцию In S (со) можно определить с помощью интеграла о

имея в виду, что при 9 (0)=0 и нормировке 5 (0) = 1 In 5 (0)=0.

Определенная таким образом функция In S (со) является однозначной.

Используем аналогичный способ устранения неоднозначности комплексного логарифма для дискретного сигнала.

Логарифмическая производная по аналогии с (16.46)

dz S(z) dz

M(z)S{z)/Si2), (16.48)

где штрих обозначает производную по г, а Y (г) = In S (г) рассматривается как г-преобразование, которое можно записать в виде ряда

У(г) = 1п5(г)= J y(m)z-". (16.49)

m= -оо

Заметим, что применив к (16.49) обратное г-преобразование, получим у (т), которое есть не что инее, как искомый кепстр (комплексный). Однако предварительно необходимо устранить неоднозначность комплексного логарифма In S (г). С этой целью продифференцируем (16.49):

Y(z)= S i-m}y{m)z--=S(z)/S(z)

т= -оо

и умножим \ (г) на г:

гУ(г)= 2 l-my(m)]z-"zS (z)/S(z).

т - -оо

Входящий в это выражение ряд по отрицательным степеням г представляет собой г-преобразование последовательности {- ту {т)}, поэтому с помощью (16.40) получаем

-ту (т) = ~. j) [zs (г)/?(г)] г""- dz,

у{т) =--- & (S {z)/S{z)] z" dz. (16.50)

2nim J

Найденное таким образом значение у (т) можно обозначать символом Cs, аналогичным обозначению кепстра мощности Cs-

Приведенные рассуждения справедливы при условии, что окружность единичного радиуса на г-плоскости входит в область сходимости функции

In S (г). Заменив контур интегрирования С на 2 = 1, перепишем (16.50) в форме

y{m) =--- f [S(e0/S~(e*n]e>("+>d(©r)=C,(m), (16.51)

Итак, комплексный кепстр найден без обращения к логарифму и, следовательно, однозначно.

При т-0 значение кепстра можно определить непосредственно из второй части выражений (16.41):

СЛО) = г/(0) = ] fn?(e--)d(«T) =

I [In 1 S"(e<)I +iargS(e<)]d(шГ).

Поскольку arg S (e**) является нечетной функцией частоты, полу-

чаем:

СЛО) = S 1п18(е-01(о)Г).

(16.5Г)

Наряду с описанным методом, основанным на логарифмической производной, широко распространен метод прямого вычисления комплексного логарифма с помощью БПФ. При этом используются соотношения 1 W-1

у{т)=- 2 lnS(n)e<2"/)«" = -i- {In S(ш)+

п=0 п=0

+ n6swiH + -2it]}e<2/W)nm m = 0, 1,..., N - \.

Главное значение аргумента 0s (ш) вычисляется на ЭВМ непосредственно с помощью стандартной программы. Это главное значение фазы затем «разворачивается» так, чтобы получились отсчеты из непрерывной ФЧХ спектра сигнала. Непрерывная ФЧХ 0s (ш) и отсчеты 0s {п Асо) показаны на рис. 16.17, а, а главное значение 0s гд (о») - на рис. 16.17, б.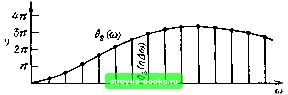

"\- б) 0

-п -

4п -

3?г-

7Т -

J I L

0 Л(г)2Лы

Рис. 16.17. Устранение неоднозначности фазы 08 (ы):

а) непрерывная ФЧХ 6s((u);

б) главная часть фазы; в) корректирующая последовательность