Напомним важное свойство контурного интеграла: он не зависит от формы замкнутого контура, по которому проводится интегрирование, если только полюсы подынтегральной функции остаются внутри контура. На основании этого свойства контур, образованный добавлением дуги ABC бесконечно большого радиуса (см. рис. 2.27, а) к прямой - гоо, + можно произвольно деформировать при соблюдении условия, что все полюсы, расположенные левее прямой - гоо, + гоо, остаются внутри контура.

Итак, вычисление интеграла (2.103) сводится к определению вычетов в полюсах подынтегральной функции.

На рис. 2.27, а показано положение полюсов для следующих функций времени:

hit) Si it)

g-aCOSCuga, i.

S3 (t)

0,

e-"sin CU02 cos Юцз t, CO,

Рг. P2 = -«2 ±

sincOo3, fO,

Рз, рд, =± Шръ-

(2.105)

(2.105)

Рассуждения, аналогичные предыдущим, можно привести для функции s (t) заданной при -оо < < 0. Домножив s () иа е""°, при о, < О, выбранной таким образом, чтобы обеспечивалась абсолютная интегрируемость функции e~02s g пределах -оо <; < < О, можно написать

Ls-(p)= I «-(Ое-е-й f s (Oe

(2.106)

02 + too

s- (t) -

2л (

Ls- (/>) ePdp.

(2, 107)

02 - too

Контур интегрирования для данного случая показан на рис. 2.28. Интеграл равен сумме вычетов в полюсах функции Lg- (р) еР, расположенных в правой полуплоскости р. Эту сумму следует взять со знаком минус, поскольку при t < О контур обходится по часовой стрелке.

Выражения (2.102), (2.106) и (2.101), (2.107) можно объединить следующим образом :

Ls {р)=и+ (P) + Ls-. (р)

s(0 =

-i-ioo

Ls+ (р) ePdp +

Ls- (p) eP dp

(2.108)

(2.109)

Соотношение (2.108) называется двусторонним преобразованием Лапласа.

Области сходимости функций Ls+ (р) и Ls- (р) на плоскости р показаны на рис. 2.29. Для Ls- (р) эта область расположена справа от прямой а = -а, на которой расположены полюсы (комплексно-сопряженные), а для Ls~ (р) - слева от прямой ст = IojI. Область сходимости для I.s (р) имеет вид полосы шириной OiIctjI.

Путь интегрирования должен проходить по прямой, расположенной внутри этой полосы и параллельной оси ш, а также по замыкающей дуге, расположенной в левой полуплоскости для > О и соответственно в правой полуплоскости для / < 0.

Одностороннее преобразование Лапласа получило особенно широкое распространение при анализе переходных процессов, связанных с действием на цепь внешней силы, когда начало отсчета времени совмещают с началом воздействия. Двустороннее преобразование Лапласа находит все большее применение при анализе процессов и функций времени, двусторонних по самой своей сути (например, корреляционных функций, рассматриваемых в §2.18).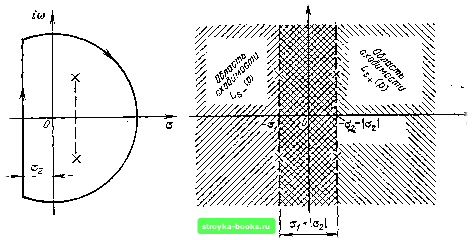

Рис. 2.28. Замыкание контура интегрирования для представления функции s-.{t) при <0

Рис. 2.29. Области сходимости при двустороннем преобразовании Лапласа

* При рассмотрении четных функций s (О = s {-t), когда можно считать s+ (t) = = s (-имеет место следующее соотношение:

Is-(P)= J s(Oe~Pd/= [ s(-Oe-<-d(-0= j" s(Oed/ =

- OO oo 0

Ls+(-p). (2.110)

Поясним применение выражений (2.106)-(2.110) на двух примерах.

1. Четная функция s {t)= е""при а > О (рис. 2.30). По формулам (2.102) и (2.110) находим

Ls+ (р) = !/(а + р), Ls- (р) = 1 /(а-р). Тогда

Z.S (Р) = 1 /(а + р) + 1 /(а -р) = 2а/(а2-р2).

(2.111)

2. Прямоугольный импульс при отсчете времени от фронта (см. рис. 2.16) или от середины импульса (см. рис. 2.14, а). В первом случае

Lsip) = il/p){l-t-»). Во втором случае LsiP)-l-s+ (P)+is- (Р),

t,+ (p)= - (l-e-PV); Ls-{p) = Ls+{-p) = .(i e+PV2).

Рис. 2.30. Пример функции времени, требующей применения двустороннего преобразования Лапласа

Таким образом,

1«(р) = (1/р)(еРи/2 е-и/2). (2.112)

Большинство свойств преобразования Лапласа совпадает с аналогичными свойствами преобразования Фурье, изложенными в § 2.8. Если сигналу s (t)

соответствует изображение по Лапласу Ls (р), то имеются следующие соответствия:

S (/- g е-Р« L, (р), S (О е-« ~ L, (/ + а),

S (О е"»о -Lsip- s (t) cos ©0 4- V2L, (p - /(Oo) + V2L, (p -f 14), t 00

pLC/), 8(0Л-(1/Р)1Лр). j Si(t/)s2(-i/)d(/L,(p)L2(p).

0 -00

В заключение остановимся на правилах перехода от изображения Лапласа к преобразованию Фурье S (со) (имеются в виду односторонние преобразования Лапласа).

Если на оси tco функция Ls (р) не имеет полюсов, то для такого перехода достаточно в (2.102) положить а, = О, т. е. перейти от переменной р к переменной ко. В противном случае, чтобы избежать ошибки, необходимо определить вклад этих полюсов в спектральную плотность cигнaлa.

Дело в том, что интегрирование функции Lg (р) еР по полуокружности бесконечно малого радиуса с центром в полюсе pi == ico приводит к гармоническому колебанию с частотой coi и амплитудой 1/2. Спектральная плотность такого колебания, равная лб (со - coj), должна быть прибавлена к сплошному спектру, обусловленному интегрированием по оси ш.

Так, для функции Ls (р) с одним полюсом в точке Pi = О [s (О = 1, t > О) мы ранее получили

S(co) =лб(со) J 1/ко;

для функции Ls (р) с двумя комплексно-сопряженными полюсами pi, = = +ICO0 Is (t) = cos cOq, t > 0] спектральная плотность будет

S (0)) = л [б (со-со„) + б (со + С0о)1 (2.113)

и т. д. (см. приложение 1).

Изображения по Лапласу и соответствующие им спектры Фурье некоторых распространенных в теории сигналов функций приведены в таблице 2.1.

2.15. ПРЕДСТАВЛЕНИЕ СИГНАЛОВ

С ОГРАНИЧЕННОЙ ПОЛОСОЙ ЧАСТОТ В ВИДЕ

РЯДА КОТЕЛЬНИКОВ\

В теории и технике сигналов широко используется теорема Котельни-кова (теорема отсчетов): если наивысшая частота в спектре функции s (t) меньше, чем fm, то функция s {t) полностью определяется последовательностью своих значений в моменты, отстояш,ие друг от друга не более чем на l/2/m секунд.

В соответствии с этой теоремой сигнал s {t), ограниченный по спектру наивысшей частотой oj = 2я/т, можно представить рядом

в этом выражении i/2/ni = обозначает интервал между двумя отсчет-ными точками на оси времени, а s (п/2/m) = s (nAt) - выборки функции S (t) в моменты времени t = nAt.

iQm.: Троиии Ю. В. Утеряна дельта-функция! -Радиотехника и электроника, 1986, №2, с. 408.