тельно своей копии сдвигать сигнал на величину т. Поэтому выражение (2.129) можно обобщить следующим образом:

В,, (т)

S (/) S {t 4- т) dt = Г S (t) S (t -т) dt.

(2.129)

Это равносильно утверждению, что Bs (т) является четной функцией т. На рис. 2.38, а показан сигнал в виде пачки из четырех одинаковых импульсов, сдвинутых один относительно другого на время Т, а на рис. 2.38, б - соответствующая этому сигналу корреляционная функция. Вблизи значений т, равных О, iTb +2Г1 и ±37,, эта функция имеет такой же вид, как и для одиночного импульса (см. рис. 2.36, г). Максимальное значение корреляционной функции (при т = 0) равно учетверенной энергии одного импульса.

Для периодического сигнала, энергия которого бесконечно велика, определение корреляционной функции с по.мощью выражений (2.129) или (2.129) неприемлемо. В этом случае исходят из следующего определения:

г/2 Г/2

B,„p(T)=!im - \ s(t)s{t \ x)dt =\\т- Г s (t-т) s [t) dt.

-r/2 --Г/2

(2.131)

При таком определении корреляционная функция приобретает размерность мощности, причем Вр (0) равна средней мощности периодического сигнала. Ввиду периодичности сигнала s {f) усреднение произведения s (/) х X S (/* Ч- т) или S (t - т) S {t) по бесконечно большому отрезку Т должно совпадать с усреднением по периоду Г,. Поэтому выражение (2.131) можно заменить выражением

г,/2 f, 2

.4 пер

(т) = - Г s(/)s(/-J-T)d/=- f s (t) s (t-X) dt.

7,.2 -r,/2

(2.132)

Входящие в это выражение интегралы суть не что иное, как корреляционная функция сигнала на интервале Г,. Обозначая ее через Вт, (т), приходим к соотношению

B.«„op(T)=Bsr, (т)Т,.

Очевидно также, что периодическому сигналу s (t) соответствует и периодическая корреляционная функция В., „р (т). Период функции В, „ер {)

s(t)

П □ □ □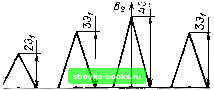

Рис. 2.38. Пачка из четырех прямоугольных импульсов (а) и корреляционная функция (б)

совпадает с периодом исходного сигнала s (t). Например, для простейшего (гармонического) колебания s (t) = А(, cos {u)„t + ва) корреляционная функция

5..пер (ч) = f COS (СО,, / + Во) COS [oj„ (/ т) -1- Оо1 dl =

-Г,/2

1 ,., 2л =- Л о COS со,, Т, сОц = - .

При т - о S.S ,ц.р (0) Лб есть средняя мощность гармонического

колебания с амплитудой Л,,. Важно отметить, что корреляционная функция Bs j,gp (т) не зависит от начальной фазы колебания Вц.

На рис. 2.39, б изображена корреляционная функция сигнала, представляющего собой периодическую последовательность прямоугольных импульсов (рис. 2.39, а). Каждый из импульсов функции Вр (т) совпадает по форме с корреляционной функцией одиночного импульса из периодической последовательности s (t). Однако в данном случае максимальные ординаты Bsngp (т) равны не энергии (как на рис. 2.38), а средней мощности

сигнала s (t), т. е. величине S (t).

Для оценки степени связи между двумя различными сигналами (t) и s, (t) используется взаимная корреляционная функция, определяемая общим выражением

Для вещественных функций s, (t) и (/) ,,s,(T)= ( Sy{t}s.(t-rT)dt.

(2.133)

(2Л34)

Рассмотренная выше корреляционная функция В., (т) является частным случаем функции Bs,s, (т), когда s, (t) s„ (t).

Построение взаимной корреляционной функции для двух сигналов Si (t) и So (/) приведено на рис. 2.40. Исходное положение сигнала т О показано на рис. 2.40, а. При сдвиге сигнала s., (t) влево (т > О, рис. 2.40, б) корреляционная функция сначала возрастает, затем убывает до нуля при т Т. При сдвиге вправо (т <: 0) корреляционная функция сразу убывает.

В результате получается асимметричная относительно оси ординат функция В,, (т) (рис. 2.40, в).

Очевидно, что значение Bjs, не изменится, если вместо упреждения сигнала s. {t) дать задержку сигналу S, (/). Поэтому выражение (2.134) можно обобщить следующим образом:

- ( S2(?)si(-T)d/=B,,,„ (- т).

(2.135)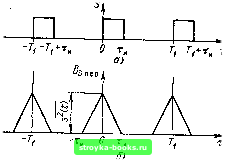

Рис. 2.39. Периодическая иоследоаате.ь-ность импульсов (а) и ее корреляционная функция (б)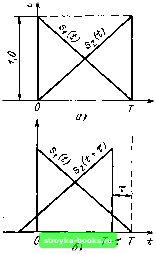

Рис. 2.40. Построение взаимной корреляционной функции:

й) исходное положение сигналов; 6) сдвиг сигнала на Т; в) взаимная корреля-

ционная функция

Соответственно

Ss,s, (T) = fis,s, ( т).

(2.135)

Следует, однако, различать выражения (2.129) и (2.135). В отличие от Д, (т) взаимная корреляционная функция не обязательно является четной относительно т. Кроме того, взаимная корреляционная функция не обязательно достигает максимума при т = 0. Оба эти свойства функции Bj.tj (т) иллюстрируются рис. 2.40.

2.19. СООТНОШЕНИЕ МЕЖДУ КОРРЕЛЯЦИОННОЙ ФУНКЦИЕЙ И СПЕКТРАЛЬНОЙ ХАРАКТЕРИСТИКОЙ СИГНАЛА

Воспользуемся выражением (2.63), в котором положим / (/) = s (/), g (i) = s (М т) и соответственно F ((о) = S ((о), G (<а) = S (ш) е-"". Тогда получим

s(/)s(/-f т) dl =

j S(w)S*(

ю) е"" da--B (т).

Учитывая, что S (со) S* (ш) - S (со), приходим к искомому соотношению

В, (т)=- Г Sco) е-""тЛо. (2.136) 2л j

- X.

На основании известных свойств преобразований Фурье можно также написать.

А.

(to) = \ В, (т) е"" dl. (2.137)

Вследствие четности функции В, (т) знак перед /шт в показателе степени может быть произвольным. То же относится к (2.137).