
 |
|
Главная Цепи и сигналы [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [ 25 ] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] [167] [168] [169] дуляции 2Q, а амплитуды колебаний боковых частот не могут Г1ревып1ать половины амплитуды немодулированного колебания (при М < 1). Аналогичные результаты можно получить при модуляции любым сложным сигналом. Картину образования спектра амплитудно-модулированного колебания проще всего пояснить сначала на примере, когда модулирующее сообщение s (t) является суммой колебаний двух тонов: S (t) Si cos Q,t 1- Si cos QJ. По аналогии с выражением (3.5) получаем А (t) =-Л„ т АЛ„„ cos а, t АА,„, cos У., / = Л,, (1 4- ,V1, cos У, / --f /Ма cos Q.2 /). Подставляя это выражение в уравнение (3.4) и используя тригонометрические преобразования, аналогичные тем, которые были проведены при получении уравнения (3.8), приходим к следующему результату (начальные фазы несущего и модулирующих колебаний здесь для упрощения опущены): а (О = Л„ cos uj„ t -f cos (OJ, + Q,) / -\ - cos (ш, -Q,) t f + cos (0-.0 Уо) / 1 COS (<0„-Q.j) Из полученного выражения следует, что каждой из частот и Q, соответствует своя тональная модуляция, сопровождающаяся возникновением пары боковых частот, причем этот процесс является линейным в том смысле, что амплитуды и фазы колебаний боковых частот от различных модулирующих напряжений взаимно независимы (последнее свойство сохраняется при условии, что суммарное изменение огибающей «вниз» не превышает 100 %). Из приведенного примера нетрудно вывести правило построения спектральной диаграммы амплитудно-модулированного колебания а (t) по заданному спектру модулирующей функции s {t). Пусть последний имеет вид. f /К \ 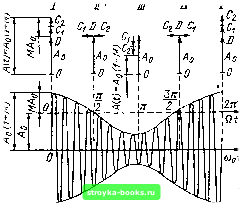 Рис. 3.5. Векторная анаграмма .4М при начальной фазе несущего колебания й = 90° Рис. 3.6. Фазы колебаний боковых частот в различные момента времени
Рис. 3.7. Спектр колебания при тональной (гармонической) AM 1ц , 1 2 MfAo Е С! 3 3 2 3 Рис. 3.8. Дискретные спектры: а) сложной моду.лирующей функции; б) модулированного по амплитуде колебания представленный на рис. 3.8, а. Через 5,, S.j, ...,Sn, ... обозначены амплитуды гармонических колебаний, входящих в спектр сообщения s [t), а через йпцп и Qniax - граничные частоты спектра. Спектральная диаграмма высокочастотного колебания, промодулирован-ного по амплитуде сообщением s (t), изображена на рис. 3.8, б. Коэффициенты модуляции Ml, М2, М„ пропорциональны амплитудам Si, S, Si, соответствующих тонов, входящих в сложное сообщение s (t). Перейдем к общему случаю, когда спектр сообщения s (t) не обязательно дискретный. Будем исходить из общего выражения (3.4). Передаваемое сообщение S (t) содержится в законе изменения огибающей А (t). Не предрешая вида функции s {/), составляем выражение для спектральной плотности Sa (м) модулированного по амплитуде колебания а (t), рассматриваемого как произведение огибающей А (t) на гармоническое колебание cos (wo + + во). Основываясь на соотношении (2.58), в котором положим s (t) - А (t), получаем S„ (ш) = J Л (/) cos (0.0 / -t В„) е-»" dl = S4 (м - <•)„). (3.9) В этом выражении 5л обозначает спектральную плотность огибающей, т. е. модулирующей функции. Следует подчеркнуть, что спектр медленно меняющейся функции времени А (t) концентрируется в области относительно низких частот. Поэтому функция Sa (о) - соо) существенно отличается от нуля лишь при частотах О), близких к о)о, т. е. когда разность м - = Q относительно мала. Аналогично слагаемое Syi (со + сод) существует при частотах, близких к -со. Таким образом, спектральная плотность модулированного колебания S„ (со) образует два всплеска: вблизи со = coq и вблизи со - -со. Поэтому для узкополосного сигнала можно считать, что в области положительных частот /.>е"» S„ (со) « /,е«- Sa ((о-(о,), . а в области отрицательных частот S„ (со « .дС "«Зд (со I (0„). (3.10) (3.10) Поясним правило построения спектра S„ (oj) на следующем примере. Пусть огибающая высокочастотного колебания имеет вид (3.11) где 5 (t) - передаваемое сообщение, имеющее спектральную плотность S (Q), а коэффициент кцм имеет тот же смысл, что и в выражении (3.5). Спектральная плотность огибающей А (t) изображена на рис. 3.9, а. Дискретная часть этого спектра, равная 2nA(,8(Q), соответствует постоянной величине Aq, а сплошная часть йамо5 (У) - передаваемому сообщению S (t). Спектральная плотность S„ (со) модулированного колебания а (/) показана на рис. 3.9, б. В данном случае дискретные составляющие пАдЬ (м + =F «о) отображают несущее колебание Л, cos (w,/ 4- б,,), а сплошной спектр - колебания боковых частот модуляции. Если радиосигнал не содержит несущего колебания (с конечной амплитудой), например, при передаче одиночного радиоимпульса, дискретная часть в спектре отсутствует. Рассмотрим спектр прямоугольного радиоимпульса (рис. 3.10, б), определяемого выражением * О при f <-т„/2 и / > т,,,/2. (3.12) В данном примере под сообщением s (t) следует подразумевать видеоимпульс (рис. 3.10, а). Спектральная плотность подобного сообщения (см. (2.68)1 Qt„/2 Огибающая амплитуд колебания о (t) Л(0-*ям Ags(t), а спектральная плотность этой огибающей (й) Л S (Q) =feaM Л В (3.1.3) -0)п Рис. 3.9. Спектральные плотности: а) огибающей: б) амплитудно-модулированного колебания 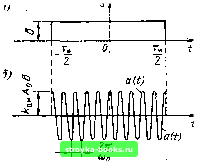 Рис. 3.10. Импульс прямоугольной формы (я) и тот же импульс с высокочастотным заполнением Мо (б) Как отмечалось в сноске на с. 72, текущая частота спектра модулирующей функции обозначается чере.з И. [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [ 25 ] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] [167] [168] [169] 0.0015 |