
 |
|
Главная Цепи и сигналы [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [ 26 ] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] [167] [168] [169] Так как в данном* случае 6о О (рис. 3.10, б), то по формуле (3.9) Sa(o>)-=- An В sin- (Ю-Шо) х„ (Ю -Юо) Хи (co-f-wo) г„ (Ю + Юо) Хи «л (3.14) Рис. 3.11. Спектральные плотности функций, представленных на рнс. 3.10 Графики спектральных плотностей модулирующей функции s (t) и радиоимпульса а (t) изображены на рис. 3.11, а и б. 3.4. УГЛОВАЯ МОДУЛЯЦИЯ. ФАЗА И МГНОВЕННАЯ ЧАСТОТА КОЛЕБАНИЯ Для простого гармонического колебания ajt) = Л о cos (aJ + Оо) Ад cosij; (t) набег фазы за какой-либо конечный промежуток времени от t=ti до равен (<г) - t (i) = («02 + So) - («01 t So) = «0 (2 - il)- (3.15) Отсюда видно, что при постоянной угловой частоте набег фазы за какой-либо промежуток времени пропорционален длительности этого промежутка. С другой стороны, если известно, что набег фазы за время to - t равен ij) (2)-15 (ti), то угловую частоту можно определить как отношение «о = Н (2)- ()1/(2- i), (ЗЛ6) если, конечно, имеется уверенность, что в течение рассматриваемого промежутка времени частота сохраняла постоянное значение. Из (3.16) видно, что угловая частота есть не что иное, как скорость изменения фазы колебания. Переходя к сложному колебанию, частота которого может изменяться во времени, равенства (3.15), (3.16) необходимо заменить интегральным и дифференциальным соотношениями xp(t.-y(ti)=\a(l) dt, t. со(0 = ci (/) (3.17) (3.18) В этих выражениях со (/) = 2я/ (t) - мгновенная угловая частота колебания; / (t) - мгновенная частота. Согласно выражениям (3.17), (3.18) полную фазу высокочастотного колебания в момент t можно определить как г15(/)= { M{t)dt% (3.19) 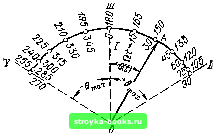 где первое слагаемое в правой части определяет набег фазы за время от начала отсчета до рассматриваемого момента t; - начальная фаза колебания (в момент t = 0). При таком подходе фазу г) (t) = = -h 9 {t), фигурирующую в выражении (3.1), следует заменить на (t) = щt+Q it) + 9о. Итак, общее выражение для вы сокочастотного колебания, амплитуда которого постоянна, т. е. А (t) Л о, а аргумент i5 (t) модулирован, можно представить в форме а (О = Ло cos [юо< + е (О + 9о]. (3.20) Соотношения (3.18), (3.19), устанавливающие связь между изменениями частоты и фазы, указывают на общность двух разновидностей угловой модуляции - частотной и фазовой. Поясним соотношения (3.18)-(3.20) на примере простейшей гармонической ЧМ, когда мгновенная частота колебания определяется выражением Рис. 3.12. Представление высокочастотного колебания при угловой модуляции в виде качающегося вектора Ю (t) Шо -! <)д COS Qi, (3.21) где Юд = 2л/д представляет собой амплитуду частотного отклонения. Для краткости Юд в дальнейшем будем называть девиацией частоты или просто девиацией. Через соо и Q, как и при AM, обозначены несущая и модулирующая частоты. Составим выражение для мгновенного значения колебания (тока или напряжения), частота которого изменяется по закону (3.21), а амплитуда постоянна. Подставляя в (3.19) со {() из уравнения (3.21), получаем t 1з (t) - f (соо + Юд cos Ш) dt + 9п. Выполнив интегрирование, найдем (t) = юо/ + (сод/й) sin Qt + 9„. Таким образом, а (t) = .4о cos [соо? -f (Юд/Й) sin Qt -f 9о1. (3.22) (3.23) Фаза колебания а (t) наряду с линейно-возрастающим слагаемым «о (О содержит еще периодическое слагаемое (Юд/Q) sin Qt. Это позволяет рассматривать а (t) как колебание, модулированное по фазе. Закон этой модуляции является интегральным по отношению к закону изменения частоты. Именно модуляция частоты по закону Юд cos Qt приводит к модуляции фазы по закону (cOg/Q) sin Й. Амплитуду изменения фазы етах = Юд/Й=т (3.24) часто называют индексом угловой модуляции. Заметим, что индекс модуляции совершенно не зависит от средней (не-модулированной) частоты Юо, а определяется исключительно девиацией Юд и модулирующей частотой й. Рассмотрим теперь противоположный случай, когда стабильное по частоте и фазе колебание пропускается через устройство, осуществляющее периодическую модуляцию фазы по закону Э (t) = 9j„ax sin Q, так что колебание на выходе устройства имеет вид ait) =ЛоС05[Шо< 4-ennaxSinQ + eo]. (3.23) Какова частота этого колебания? Используя выражение (3.18), находим со (t) = - (Шо t + бтах sin -f- Эо) = ООо + Этах 2 COS (3.21) Учитывая соотношение (3.24), приходим к выводу, что бах = сОд. Таким образом, гармоническая модуляция фазы с индексом тах эквивалентна частотной модуляции с девиацией оОд = eax- Из приведенного примера видно, что при гармонической угловой модуляции по характеру колебания нельзя заключить, с какой модуляцией мы имеем дело - с частотной или фазовой. В обоих случаях вектор OA, изображающий на векторной диаграмме модулированное колебание, качается относительно своего исходного положения таким образом, что угол 8 (рис. 3.12) изменяется во времени по закону 8 = Эах sin Qt при фазовой модуляции, Э = (сОд/Q) sin Qt при частотной модуляции (когда Д оо = = СОд cos Q. Цифрами I, И, П1 и IV отмечено положение вектора OA при Qt = О, л/2, л и Зя/2. Иное положение при негармоническом модулирующем сигнале. В этом случае вид модуляции - частотной или фазовой - можно установить непосредственно по характеру изменения частоты и фазы во времени. Локажем это на примере пилообразного модулирующего сигнала s (t) (рис. 3.13, а и г). Очевидно, что пилообразное изменение о) (t) (рис. 3.13, б),
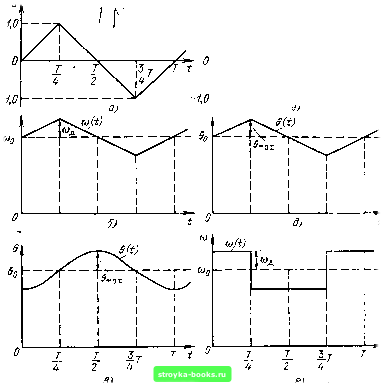 Рис. 3.13. Сравнение функций (о(/) и Н(/) при ЧМ и ФМ при пилообразном модулирующем сигнале [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [ 26 ] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] [167] [168] [169] 0.0013 |