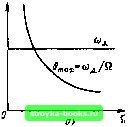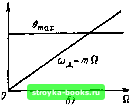Рнс. 3.14. Зависимость индекса Ншах и девиации сад от модулирующей частоты при ЧМ (а) н ФМ (б)

ПО форме совпадающее с s (t), свидетельствует о наличии ЧМ, а такое же изменение Э (t) (рис. 3.13, д) - о наличии ФМ. Ясно также, что скачкообразное изменение со (t), совпадающее по форме с производной сигнала s (t) (рис. 3.13, е), указывает на ФМ.

При гармоническом модулирующем сигнале различие между ЧМ и ФМ можно выявить, только изменяя частоту модуляции.

При ЧМ девиация сОд пропорциональна амплитуде модулирующего напряжения и не зависит от частоты модуляции Q.

При ФМ величина бтах пропорциональна амплитуде модулирующего напряжения и не зависит от частоты модуляции Q.

Эти положения поясняются рис. 3.14, на котором показаны частотные характеристики величин сОд и Эп,ах при частотной и фазовой модуляциях. В обоих случаях предполагается, что на вход модулятора подается модулирующее напряжение с неизменной амплитудой U, а частота Q изменяется от

Йт1п ДО Qmax-

При ЧМ СОд, зависящая, как указывалось выше, только от амплитуды и, будет постоянной величиной, а индекс модуляции т - сОд Q = бтах с увеличением частоты будет убывать (рис. 3.14, а). При ФМ т не зависит от Q, а СОд = бщахй = ffiQ изменяется пропорционально частоте модуляции (рис. 3.14,6).

Кроме структуры колебания (при модуляции сложным сигналом) частотная и фазовая модуляции различаются и способом осуществления. При ЧМ обычно применяется прямое воздействие на частоту колебаний генератора. При ФМ генератор дает стабильную частоту, а фаза колебания модулируется в одном из последующих элементов устройства.

3.5. СПЕКТР КОЛЕБАНИЯ ПРИ УГЛОВОЙ МОДУЛЯЦИИ. ОБЩИЕ СООТНОЩЕНИЯ

Пусть задано колебание a{i) = Ао cos [сооЧ- е (1,

(3.25)

о котором известно, что передаваемое сообщение s (t) заложено в функцию 6 (t). Если колебание а (t) получено с помощью ФМ, то 6 (?) и s (t) полностью совпадают по (}юрме и отличаются лишь постоянным коэффициентом. При этом, очевидно, с точностью до постоянного коэффициента совпадают и спектры функций 8 (?) и s (t).

При ЧМ функция Э (?) является интегралом от передаваемого сообщения s (t). Это вытекает из выражений (3.19) и (3.20). Так как интегрирование является линейным преобразованием, то при ЧМ спектр функции 9 (?) со-

стоит из тех же компонентов, что и спектр сообщения s (t), но с измененными амплитудами и фазами.

Отвлекаясь от способа осуществления угловой модуляции - фазовой или частотной - и считая заданным спектр функции 8 (г"), находим спектр модулированного колебания а (t). Для этого выражение (3.25) преобразуем к виду

а (t) = Ао cos е (t) cos соо t -Ао sin 8 (t) sin coo t = 0 (t) -Us (t). (3.26)

Из (3.26) следует, что модулированное по углу колебание можно рассматривать как сумму двух квадратурных колебаний: косинусного а (t) = = Ао cos 9 (t) cos Wot и синусного as (t) = Ао sin 8 (t) sin coot, каждое из которых модулировано только по амплитуде; закон AM для косинусного колебания определяется медленной функцией cos 9 (t), а синусного - функцией sin 9 (t). Но в § 3.3 было установлено, что для определения спектра амплитудно-модулированного колебания достаточно сдвинуть на частоту Юо спектр огибающей амплитуд. Следовательно, для нахождения спектра колебания а (t), определяемого выражением (3.26), необходимо сначала найти спектры функций cos 9 (t) и sin 9 (t), т. е. спектры огибающих квадратурных колебаний. Перенос этих спектров на частоту можно затем осуществить таким же образом, как и при обычной АЛ1.

Из приведенных рассуждений следует, что при одном и том же передаваемом сообщении спектр колебания, модулированного по углу, значительно сложнее, чем спектр модулированного по амплитуде. Действительно, так как cos 8 (t) и sin 9 (t) являются нелинейными функциями своего аргумента 9 (t), то спектры этих функций могут существенно отличаться от спектра функции 8 (t); возможно возникновение кратных и комбинационных частот, как это имеет место при обычных нелинейных преобразованиях спектра.

Это обстоятельство, а также наличие двух квадратурных слагаемых показывают, что при угловой модуляции спектр модулированного колебания нельзя получить простым сдвигом спектра сообщения на величину несущей частоты Юо, как это имеет место при АЛ1. При угловой модуляции связь между спектрами сообщения и модулированного колебания оказывается более сложной.

3.6. СПЕКТР КОЛЕБАНИЯ ПРИ ГАРМОНИЧЕСКОЙ УГЛОВОЙ МОДУЛЯЦИИ

Используем полученные выше результаты для анализа колебания вида а (t) = Ао cos {(Oot + т sin Qt). (3.25)

Это выражение совпадает с (3.23) и (3.23) при модуляции частоты по закону ю (t) = Юо + Юд cos Qt. Начальная фаза 8о, а также начальная фаза модулирующей функции у опущены для упрощения выкладок. При необходимости они легко могут быть введены в окончательные выражения.

В данномслучае Q (t) = т sin Qt. Подставляя 6 (t) в выражение (3.26), получаем

а (t) = Ао cos (т sin Qt) cos Wot- Ад sin (m sin Qt) sin Wot. (3.27)

Учитывая, что множители cos (m sin и sin (m sin Qt) являются периодическими функциями времени, разложим их в ряд Фурье.

В теории бесселевых функций доказываются следующие соотношения:

sin (m sin Qt) 2Л (m) sin + 2 У3 (m) sin 3Qt + 2J, (m) sin 5Qf + ... ,(3.28)

COS (m sin ЙО = Уо (m) + 22С") cos 2Qt + 2J ( m) cos AQt + ..., (3.29)

sin (m cos Qi) 2 (m) cos fi/ -2Jg (m) cos 3fi? -f-2J(m) cos5Q/ -...,(3.28)

cos (m cos Qt) = Уо (0 -2Л (m) cos 2Й? + 2У4 (m) cos 4Q?-... (3.29)

Здесь Jn (tn) - бесселева функция первого рода «-го порядка от аргумента т.

С помощью соотношений (3.28) и (3.29) уравнение (3.27) можно привести к виду

а (t) •= Ао [Jo (т) cos со, / -2У, (т) sin Qt sin сод t + 2У2 i") cos 2Q? cos (Oo ~~ - 2y3(m)sin3Q?sin(Oo?-f...] (3.30)

или в более развернутой форме

а (t) = Ао cos (юо ? -f m sin Qt) Яо {Л (/") cos Wot-\-Ji (tn) [cos (cOp + Q)t -

-cos (tOo - Й) ] +2 (m) [cos (o)« Ч- 2Q) i-f cos (со» - 2Q)

-f y3(m)[cos(roo-f 3Q)? -cosfoo-3Q)?]-b...}. (3.31)

Таким образом, при частотной и фазовой модуляциях спектр колебания состоит из бесконечного числа боковых частот, расположенных попарно симметрично относительно несущей частоты .соц и отличающихся от последней на nQ, где п - любое целое число. Амплитуда п-й боковой составляющей А„ - Jj, (т.) Ао, где Ао - амплитуда немодулированного колебания, am - индекс модуляции. Отсюда следует, что вклад различных боковых частот в суммарную мощность модулированного колебания определяется величиной т.

Рассмотрим режимы угловой модуляции при малых и больших значениях т. Если т < I, так что имеют место приближенные равенства

sin (т sin Qt) « т sin Qt, cos (m sin Qt) л; 1, TO выражение (3.27) переходит в следующее:

a{t) w /4о(со5Юо? - msin Qsinooo t) = Ao

--cos (coq-Q)t

cos Юо i + cos (0)0 -\-Q)t -

(3.32)

Сравним это уравнение с уравнением для амплитудно-модулированного колебания, у которого модулирующая функция (т. е. передаваемое сообщение) такая же, как и при ЧМ. Так как выражение (3.32) получено из (3.25) для модуляции частоты по закону со (t) = Wq + Юд cos Qt, то для удобства сравнения зададим модуляцию амплитуды по аналогичному закону А (t) = = Ао (1 + М cos Qt). Тогда амплитудио-модулированное колебание запишется в форме

«ам it)-=Ao(l+M cos Qt) cos COo ? =- Ио + - cos {o\-Q)t

COS COo t-\,--COS (coo + Q) t +

(3.33)

Из сравнения (3.32) и (3.33) видно, что при малых значениях т спектр колебания, как и при AM, состоит из несущей частоты соо и двух боковых частот: верхней соо -f- Q и нижней со, - Q. Единственное отличие заключается в фазировке колебаний боковых частот относительно несущего колеба-