Часто символ Re или Im опускают и пишут просто о(0=Л е=А„е""".

подразумевая действительную или мнимую часть этого выражения.

Такое представление позволяет использовать преимущ,ества методов теории функций комплексной переменной с последующим возвратом в конце анализа к тригонометрической форме путем отбрасывания мнимой части.

В современной радиотехнике представление колебаний в комплексной форме распространено на негармонические колебания.

Если задан физический сигнал в виде действительной функции а (t), то соответствующий ему ко.мплексный сигнал представляется в форме

z„ it) = а (О 4 ш, (t), (3.85)

где «1 (t) - функция, сопряженная по Гильберту сигналу а (t).

Заметим, что и в выражении (3.84) мнимая часть комплексной функции является функцией, сопряженной по Гильберту действительной части.

Главная особенность определенного таким образом ко.мплексного сигнала заключается в том, что его спектральная плотность

Za(w)---S„(M)4-iS„,(«) (3.86)

содержит только положительные частоты. Действительно, согласно (3.68), (3.69) при (о> О S„, (со) = -(S„ (сл), а при со < О S„, (со) = iS„ (w). Следовательно,

Z„(co) = P" при со > О, 0 при 0X0.

Так, если узкополосному сигналу а (t) соответствует спектральная плотность S„ (со), модуль которой изображен на рис. 3.26 штриховой линией, то сигналу Za (i) = а (t) + ia (t) соответствует спектральная плотность (со), модуль которой изображен на том же рисунке сплошной линией.

Интеграл Фурье для сигнала z„ (i) принимает следующий вид:

ос оо

г„ (t) = -i- Г Z, (со) е<" Ло = Г 2S„ (со) е"" dco, (3.88)

2я ,! 2я J

где So (со) - спектральная плотность исходного (физического) сигнала а (t).

Комплексный сигнал, определяемый выражениями (3.85) и (3.86), называется аналитическим сигналом.

Смысл термина «аналитический сигнал» заключается в том, что при переходе к переменной / = дг -1- it/ функция z„ (t) = г„ (х + iy), определяемая в соответствии с

• °

(3.88) интегралом - 1 2S„ ((о) е"""е"" (1м. является аналитической функцией для

2 л J о

каждого у > 0. Для доказательства определим энергию сигнала z„ (х + iy) с помощью равенства Парсеваля

Эг= {[2Sr, (со) е "Р dio < 25„. (>

Как видим, множитель еобеспечивает сходимость интеграла при любом у > 0. поскольку О) > 0. В случае же действительного сигнала а (t) переход к а (х + iy) приводит к бесконечному возрастанию множителя е""" в области О) <; 0. Иными словами, аналитичность сигнала обусловлена тем, что в области о) <: О спектральная- плотность функции z„ (t) равна нулю.

4* 99

Пусть задан физический сигнал

а (О = (t) cos I f 8 (t)l = A (?) cosrp (?)

и требуется определить соответствующий ему аналитический сигнал (?). Исходя из общего выражения (3.62) для сопряженной функции Oi (?) можно написать

гЛ?) = Л(?)со5г)(?)~ J

/1 (т) cos;(T) x-t

Точное определение (?) при сложной функции А (т) cosrp (т) является трудной задачей, которую можно обойти, если исходный сигнал а (?), является достаточно узкополосным процессом. Можно показать, что в этом случае

а, (?) - А (?) sin ijj (?) = Л (?) sin Uut + 8 (?) + Sol.

Таким образом, аналитический сигнал можно записать в следующем виде:

г„ (?)= А (?) е* <0 = А (?) е С» (O + e.l = А (?) е"» (3.89)

А(?)=Л (?)е[е("+бо1 (3.90)

представляет собой комплексную огибающую узкополосного сигнала.

Соотношения между А (?), а (?) и Ci (?) иллюстрируются векторной диаграммой на рис. 3.27. Модуль комплексной огибающей, равный А (?) [поскольку eC9C0-fe„] - i jjpj любом законе изменения 8 (?)], содержит информацию только об амплитудной модуляции колебания, а фазовый множитель е О - только об угловой модуляции. В целом же произведение А (?) е W содержит полную информацию о сигнале а (?) (за исключением несущей частоты «о. которая предполагается известной).

Это свойство комплексной огибающей, позволяющее при анализе узкополосных сигналов исключить из рассмотрения частоту соц, придает важное значение понятию «аналитический сигнал».

Рассмотрим основные свойства аналитического сигнала и комплексной огибающей.

1. Произведение аналитического сигнала (?) на сопряженный ему сигнал zl (?) равно квадрату огибающей исходного {физического) сигнала a{t).

Действительно,

2„ (?) Za (О «[а (t) + iai (t)\ {а (?) - 1аг (?)1 = (?) + (О (- (3-91)

Таким образом, модуль аналитического сигнала (?) равен просто огибающей сигнала А (?).

2. Спектральная плотность комплексной огибающей А(?) совпадает со смещенной на Ыо влево спектральной плотностью аналитического сигнала Za (?).

Основываясь на общей формуле (2.48), можно написать

Z„(co)- ] z,At)e""dt.

-fOg

Рис. 3.26. Соотношение между спектрами физического и аналитического сигналов

Рис. 3.27. Соотношение между амплитудой аналитического сигнала и функциями aif). o,{t)

Рис. 3.28. Соотношение между спектрами комплексной огибающей и аналитического сигнала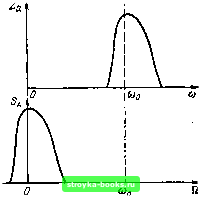

Подставляя в это выражение Zg (t) = \(t) еполучаем

с»

Z(©)= J А(0е-<«--"»)=5л(©-©о). «>0. (3.92)

Это соотношение является обобш,ением формулы (2.58) на случай комплексной функции времени А(/), умножаемой на е*» (вместо cos (Ogi в § 2.7, п. 3). Выражение (3.9), выведенное для вещественной огибающей А (() (при чисто амплитудной модуляции), является частным случаем общего выражения (3.92).

Введя обозначение ш - ©„ == Q, перепишем (3.92) в несколько иной форме

Z„ («о 4- й) = Sa (Q) = 2S„ (©о + )

(3.93)

1см. (3.87)].

Соотношение между спектрами (Q) и Za (©о + ) иллюстрирует рис. 3.28. Особо следует отметить, что спектр Sa (й) комплексной огибающей А (t) не обязательно симметричен относительно нулевой частоты (см. рис. 3.28). Если спектр Sa (оз) физического колебания а (i) несимметричен относительно й) = «о, как это может иметь место, например, при амплитудно-угловой модуляции (см, § 3.8), то и функция Za (со) = 2So (со), со > О, несимметрична: после сдвига Za (со) на величину со влево спектр комплексной огибающей (Q) будет несимметричен относительно частоты Q = 0. В любом случае функция Sa (Q) отлична от нуля в области частот Q <: 0. Следовательно, комплексная функция А (о че является аналитическим сигналом. Это объясняется тем, что действительная и мнимая части А(0 не являются функциями, сопряженными по Гильберту.

3. Корреляционная функция аналитического сигнала, определяемая общим выражением

(Т)= J Za{t)za{t + X)dt,

(3.94)

является комплексной функцией.

Действительно, выразив В (т) через модуль спектральной плотности сигнала Sa (со) с помощью выражения вида (2.136), получим