Рис. 4.14. К определению двумерной плотности вероятности квадратурных составляющих комплексной огибающей узкополосного процесса

Рис. 4.15. К определению двумерной плотности вероятностей модуля и аргумента комплексной огибающей

Вероятность того, что конец вектора А (t) лежит в элементарном прямоугольнике dAdA (рис. 4.14), равна произведению вероятностей пребывания в интервале dA и в интервале dA:

р(А,) dA,p{As) dA,

-г ехр

-)dA,dAs.

При переходе от прямоугольных координат к полярным площадь заштрихованного на рис. 4.15 элемента будет ЛбЛ, а вероятность пребыва-

ния конца вектора в этом элементе равна ехр (- ) AdQdA.

Из этого выражения следует, что двумерная плотность вероятности

р{А,д)

Г ехр

2яст,

2а ,

(4.69)

Интегрируя ло переменной Э, получаем одномерную плотность вероятности

ра (Л)= \ р (Л, 8)8=;--ехр

" <3к

0< Л<, с».

(4.70)

Обоснование пределов интеграла приводится в следующем пункте данного параграфа.

Распределение огибающей, характеризуемое плотностью вероятности (4.70), называется распределением Рэлея (рис. 4.16). Максимальное значение функции рл (Л) получаетря при Л = 0. Это означает, что А = 0Д. является наивероятнейшим значением огибающей.

Среднее же значение (математическое ожидание) огибающей

М\А\~\ара (Л)йЛ =

о1 •„

Л ехр

j dA

(4.71)

Рис. 4.16. Распределение Рэлея

5 Зак. 1326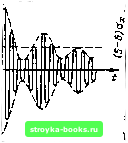

Рис. 4.17. Ширина шумовой дорожки для узкополосного нормального шума при вероятности превышения границ около 1 %

Аналогично средний квадрат огибающей

(4.72)

Этот результат совпадает с (4.65). Таким образом, средняя мощность огибающей равна удвоенной дисперсии шума. Это аналогично соотношению между квадратом амплитуды и средней мощностью гармонического колебания а (О = Ло cos СОо?, равной (?) = ЧА1.

Вероятность того, что огибающая Л (?) превысит некоторый заданный уровень С, определяется (}юрмулой

Р(Л >С) = [рл ()Л =

2а? /

(4.73)

а вероятность того, что огибающая А (?) будет ниже уровня С, - с)юрмулой Р (Л < С) = 1 - ехр (- CV2aJ). (4.74)

Из этих формул видно, что уже при С = За, вероятность превышения уровня С составляет всего лишь около 1 %. Поэтому можно считать, что ширина шумовой дорожки, фактически наблюдаемой, например, на экране осциллографа (рис. 4.17), не превышает (5 ... 6) о..

Этот результат, естественно, близок к данным, приведенным в §4.2 для шумовой дорожки широкополосного гауссовского процесса (со спектром, примыкающим к нулевой частоте).

Ковариационная функция огибающей узкополосного нормального шума [13] определяется по формуле, которую приводим без вывода:

К А (х) =

1 + К- Их)-1-

ЬЗ . . .(2rt -3)

(4.75)

Здесь Г(, (т) представляет собой огибающую нормированной корреляционной функции шума х (t), т. е. функции, определяемой выражением (при л: = 0)

г. (т) (т) al (т) cos (Оот. (4.76)

Так как Гц < 1, то ряд (4.75) быстро сходится. Поэтому можно ограничиться первыми двумя членами:

К а (г)

1 +-i-o(T) 4

(4.77)

Применяя к Ка (т) преобразование Фурье см. (4.38)1, находим спектральную плотность мощности огибающей

Wa (Q)=.2n6(Q)

5 rg (т) е-й dr.

(4.78)

Из выражения (4.78) видно, что спектр огибающей примыкает к нулевой частоте. Первое слагаемое в правой части (4.78) соответствует постоянной составляющей огибающей, а второе - сплошной части спектра.

Примеры применения формул (4.75)-(4.78) приводятся в § 11.3-11.5.

2. ФАЗА

Интегрирование двумерной плотности вероятности р (А, б), определяемой выражением (4.69), по переменной А дает одномерную плотность вероятности фазы

(4.79)

Этот результат согласуется с пределами интегрирования в (4.70). Заметим, что из представления р (А, Q) 1см. (4.69)1 в виде произведения

р(А, 6)=- ехр 2лах

2а 1

- ехр

\ 2я

= ра (Л) Ре (6)

непосредственно вытекает статистическая независимость случайных величин Л и 0. Как и в отношении А (t) и Л, (t), это справедливо при отсчете Л (t) и б (О в один и тот же момент времени 1см. замечание к (4.67)1.

Соотношения (4.70) и (4.79) позволяют сделать следующее общее заключение: произведение вида х = Л cos О, в котором Лив - независимые случайные величины, причем Л распределена по Рэлею, а б равновероятна в интервале (-я, л), обладает нормальной плотностью вероятности.

Условие узкополосности процесса х (t) не обязательно; необходимо лишь, чтобы Л и б были связаны соотношениями (4.63).

Корреляционная функция фазы В (/) определяется выражением [131

(4.80) 131