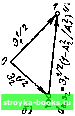Рис. 4.20. К определению расстояния между двумя ортогональными сигналами

где 7 - угол между векторами

cos 7 = •

(X, Y)

II X 11-11 Y

С учетом (4.98) и (4.99) получаем

.Э,, + Эу-2Эу, (4.100)

где Эу - «энергия взаимодействия»,.

Из (4.100) видно, что расстояние между сигнальными точками, соответствующими сигналам х (/) и у (t), зависит как от энергии каждого из сигналов, так и от взаимной корреляционной функции Вх,, (0).

Известно, что скалярное произведение можно записать в форме

(X, Y) = XHrl cos Y.

X и Y. Таким образом,

(4. ЮГ)

Используя формулы (4.98) и (4.99), записываем последнее равенство следующим образом:

Bxv (0)

cos у =

о1/2 о1/2

(4.102)

Итак, расстояние между сигнальными точками и угол между соответствующими им векторами полностью определяются энергиями сигналов х (t), у (t) и энергией взаимодействия между ними.

Проиллюстрируем эти свойства на простых сигналах. На рис. 4.20, а изображены два отрезка косинусоидального колебания одинаковой длительности Т, но с различными (кратными) частотами. Энергии сигналов: 5i = Л!Г/2 и 2 = Aim.

Оба сигнала представлены в ш-мерном пространстве (Т). Длительность сигналов равна целому числу периодов, так что взаимная корреляционная функция BsSi Ф) = Ои, следовательно, сигналы s, (nsj (/) ортогональны. Применяя формулу (4.100), находим

dl5i + = .-J (Ai + AI) = 5г(М Л?/Л?),

...•=Э}/2(1+Л/Л1)/2.

Вследствие ортогональности функций Si (t) и Sj (t) угол между векторами Si и Sj равен я/2 [см. (4.102)1. Положение сигнальных точек / и 2 (отмеченных кружками) в пространстве сигналов показано на рис. 4.20, б (положение точки О выбрано произвольно).

Рассмотрим теперь два сигнала с одинаковыми амплитудами и частотами, но с различными начальными фазами

Si (t)-=AoCosat, \ t\ Г/2,

Si (t) -= Л(, cos (cot - 0o), I / К 7/2.

Как и в предыдущем примере, Т равно целому числу периодов колебаний Si (t) и Sjj (t)\ энергии одинаковы: = = AITI2.

Взаимная корреляционная функция

TI-1 7/2

Bs, S, (0) .= j* Si (f) Sa (0 dt Ab J cos wt • cos Ш -e„) dt

- r/2 - r/2

-COS Og.

Рассмотрим частные случаи бо = О, я/4, л/2 и л.

1. во = 0; S, (0) - Al Т/2 Э{, d„= 0; cos у 1; у = 0; Сигнальные точки / и 2 совпадают.

2. во-л74; S„s, (0)=-4-

2 1 2 к 2

df,,= -25, - 2Ss.s.(0)-25,(l -l/l/t)0,293; d,,,, =0,541; cos 7 = fi,, s, (0)/5i == I /"kt; 7= л/4.

3. во=л/2; fis,sЛО) -0; dl.25,; ds,s,kt,2; cos 7 = 0; 7=-я/2.

4. в„ = л; fi,,,0)=-5,;<.s.=--25,-(-23i) = 45,; ds,s,-23}/2; cos 7= - 1; 7 - Л.

Из рассмотренного примера вытекает, что при заданной и одинаковой энергии двух сигналов любое различие в их форме не может увеличить расстояние между сигнальными точками более чем до 25}/ (это вытекает также из того факта, что сигнальные точки при заданной энергии сигнала расположены на многомерной сфере радиуса 5/2).

В заключение найдем смещение сигнальной точки, соответствующее сдвигу сигнала во времени на т. Для этого требуется определить расстояние между сигналами s, (t) и s. [t) = (t - т).

В данном случае

х- оо

fi,,,,(0) \ s,(t)s(t)dt== \ (t) sAt-Vdt Вs,{T),

- ТС --ОС

где fis, (т) - корреляционная функция сигнала Sj (t). По формуле (4.100) находим

d,,,,- {2[fi„ (O)--fi., (т>1}/2.

Если под S (t) подразумевается, например, импульс с длительностью т„, то при т > т„ корреляционная функция fi,, (т) = О и ds,s, = [2fis, (0)l/. Иными словами, неперекрывающиеся во времени сигналы ортогональны.

Применение к сигналам теории векторных пространств оказывается полезным, в частности, для синтеза цепей, подчиняющихся обобщенному принципу суперпозиции. Этот вопрос рассматривается в гл. 16.

4.9. ПРОСТРАНСТВО СЛУЧАЙНЫХ СИГНАЛОВ

Пусть рассматривается стационарный случайный процесс с дисперсией Dx, заданный на отрезке времени 0<;< Т. Без утраты общности рассмотрения положим М (х) - 0.

При представлении ансамбля реализаций в пространстве (Т) каждой из реализаций можно поставить в соответствие свою сигнальную точку, от-

стоящую от начала координат на расстоянии = Этк (см. предыдущий параграф). Энергия Этк изменяется от одной реализации к другой случайным образом, а среднее значение (математическое ожидание) энергии Эт = аТ.

Совокупность всех сигнальных точек образует сложную многомерную поверхность, тем больше отличающуюся от сферической, соответствующей среднему радиусу Rq - Эт, чем больше дисперсия Оэ = случайной величины Этк-

Для оценки величины a составим выражение для энергии k-и реализации процесса х (t)

Г ">

Эг = 4 (О dtAt 2 = S Уп 4.103)

g п= 1 п=1

где т - число отсчетов, определяющих функцию Xk (t) на отрезке Т = = m&.t (см. §2.15), а Уп ~ х1 - отсчеты мощности (мгновенной) реализации Хи (t) в моменты времени t = пМ.

Очевидно, что математическое ожидание случайной величины

т т г

п= 1 п~-1

а среднее значение квадрата 3rk в соответствии с (4.103) М (5fft)-M

т \

>: Уп

Следовательно, искомая дисперсия

т т

о=м (5Ь) - [м {Эг)Г - (мг 2 (Уп У) -itf " =

л=и=1

m т

Для конкретности будем исходить из нормального распределения процесса X (t), а также из условия взаимной независимости отсчетов у„ = х1 w У1 = . Тогда

Л (уц yi) (х1 xi) (4) /И (4)

и все слагаемые вида М (упУ1) - (т1 при пф I в выражении (4.104) обращаются в нуль. Остаются слагаемые при п =- т, число которых равно т, а сами слагаемые имеют вид М (4) - <Ух-

При плотности вероятности р (х) = (l/V2nOj.) ехр (-4/2а)

М (4) - М{х*) г х е"""" dx = Зо.

>2я а, j

- оо

Таким образом, выражение (4.104) приводится к виду Составим отношение