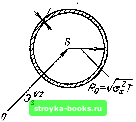Рис. 4.21. Представление в многомерном пространстве сигналов смеси детерминированного сигнала и шумовой помехи при ст7"<сЭз

yfUmRo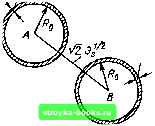

VzTmRn

Рис. 4.22. Представление двух ортогональных сигналов с шумовой помехой

Использование понятия пространства сигналов эффективно при больших базах сигнала т (сотни и тысячи). Из (4.105) видно, что при 1 отношение 1Эт настолько мало, что можно говорить о сосредоточении сигнальных точек в тонком сферическом слое радиусом = Эу и тoлщинoй

слоя около ]/"2/т R. Таким образом, в многомерном пространстве сигналов случайный процесс, отвечающий оговоренным ранее условиям (стационарность, число независимых отсчетов в интервале Т, равное т), можно пред-/ ставить в виде «тонкостенного» шара с центром в начале координат.

При совместном воздействии сигнала (детерминированного) и помехи (случайного процесса) представление суммарного колебания в пространстве сигналов основывается на правилах векторного сложения (вычитания), изложенных в предыдущем параграфе (предполагается, что сигнал и помеха представлены одинаковым числом степеней свободы т). На рис. 4.21 иллюстрируется случай относительно слабой помехи (стГ меньше энергии сигнала 9s), образующей в пространстве сигналов полый шар радиуса Rg = Ya%f с центром в точке s. соответствующей сигналу s (t) с энергией Э.

Описанное свойство многомерного пространства сигналов позволяет в наглядной форме объяснить преимущества многобазовых сигналов при решении задачи разрешения (различения) сигналов на фоне помех. Пусть на вход приемного устройства, рассчитанного на обработку двух ортогональных сигналов А {t) и В (t), обладающих одинаковыми энергией, длительностью и шириной спектра, но различной формой, воздействует смесь, состоящая из шумовой помехи и одного из указанных сигналов.

Положение сигнальных точек А (t) и В (t) в пространстве сигналов показано на рис. 4.22. Расстояние между двумя ортогональными сигналами равно "2 (см. примеры предыдущего параграфа).

В приемник тем или иным способом закладываются копии сигналов А (t) и В (t), так что в отсутствие помехи выходное устройство безошибочно принимает решение о том, какой из сигналов поступает на вход.

При наличи помехи каждый из сигналов А (t) и В (t) совместно с помехой образует в многомерном пространстве сигналов полый шар, как это изо-

1 Э.+ 05

откуда 2ДЙ/йо = аэ/5г= 2/от .

бражено на рис. 4.22. Если радиусы шаров меньше половины расстояния между точками А и В, т. е. аТ<; l> возможность безошибочно-

го различения сигналов практически сохраняется [22].

Допустим теперь, что при сохранении неизменными 5 и Г база сигнала т уменьшена. Поскольку база сигнала равна 2д/Т (см. §2.15 и 3.11), это уменьшение имеет место при сужении полосы частот сигнала. Расстояние между сигнальными точками А и В остается прежним, однако расположение сигнальных точек суммы сигнал -f помеха в пространстве сигналов «размывается», и тем сильнее, чем меньше число координат т. Вероятность «пе-репутывания» сигналов А (t) и В (t) возрастает с уменьшением базы сигнала.

Глава 5. ЛИНЕЙНЫЕ РАДИОТЕХНИЧЕСКИЕ ЦЕПИ С ПОСТОЯННЫМИ ПАРАМЕТРАМИ

5.1. ОПРЕДЕЛЕНИЯ И СВОЙСТВА АКТИВНЫХ ЦЕПЕЙ

В данной главе приводятся основные сведения о линейных активных цепях. Рассматриваются частотные характеристики избирательных цепей, используемых для различных линейных преобразований сигналов (усиления, фильтрации и т. д.). Особое внимание уделяется изучению линейных активных цепей с обратной связью, используемых в большинстве современных радиоэлектронных устройств.

В общей теории цепей под активной подразумевается цепь, сэдэржздая наряду с пассивными элементами (катушками индуктивности, конденсаторами и резисторами) также и источники энергии (генераторы ЭДС или гене-торы тока).

Активный характер цепей радиоэлектронных устройств обусловлен при -менением в них усилительных элементов: транзисторов, электронных ламп, ламп бегущей волны и т. д. При этом предполагается, что энергия сигнала на выходе активной цепи больше, чем на входе. Для большей определенности видоизменим формулировку следующим образом: цепь активна, если при гармоническом возбуждении средняя мощность сигнала на выходе больше мощности на входе, т. е. коэффициент усиления по мощности больше единицы. Из такого определения ясно, что цепь, осуществляющая усиление напряжения, например, с помощью повышающего трансформатора без усиления мощности является пассивной, даже если в нее входят активные элементы со своими источниками питания.

При построении схем замещения активных цепей источники постоянного тока или напряжения опускаются. На этих схемах активные элементы (транзисторы, лампы и др.) отображаются с помощью элементов, пара.метры которых зависят от режима работы и в конечном счете от источников энергии, питающих активный элемент. При этих допущениях любой (как активный, J так и пассивный) линейный четырехполюс-

г--[ ник можно представить схемой, изобра-

о- о. женной на рис. 5.1. На этом рисунке Ej,

о -о Еа, Ii и la обозначают комплексные ам-

плитуды гармонических напряжений и то-Рис. 5.1. Схема замещения линей- независимых источников при фикси-

ного четырехполюсника рованнои частоте со.

Четырехполюсник полностью характеризуется соотношениями между напряжениями и токами на его входе и выходе. Вид этих соотношений зависит от выбора исходных величин.

Напомним вкратце основные формы представления четырехполюсников.

Если исходными являются напряжения Ei и Eg, то уравнения для определения токов II и 1.2 записываются в форме

h-YnEi + Yi,E„ l-KnEi + yEa (5.1)

или в матричной форме

li I,

где [7]==

Yn Y22.

(5.2) (5.3)

является матрицей параметров, имеющих смысл и размерностьпроводимо-

стеи.

Если уравнение (5.1) решить относительно Ei и Е, то по.учатся системы уравнений

El = Zji Ij -f- Zj2 I2, E2 - Zj II -f- Z22 I2,

El E,

-[21 где [21 =

L I.J

L 21

(5.4) (5.5)

(5.6)

является матрицей параметров, имеющих размерность сопротивлений. Исходным уравнениям четырехполюсника, записанным в форме

El != ц II4" 12 Ег, I221 II 4"22 Е2, (5.7)

соответствует матрица параметров

Яц Я10

23 J

(5.8)

в которой Яц имеет размерность сопротивления, Я22 - проводимости, а Я12 и Я21 - безразмерные параметры. Приведем еще уравнения в форме

23 2.

[01 =

(5.9) (5.10)

Ii"Gu Ei-f Gi2 I2, E2=.G2iEi которой соответствует матрица Gn G12 G.21 G22.

где Gil - проводимость; G22 - сопротивление, а G12 и G21 - безразмерные параметры.

В теории усилителей наибольшее распространение получили матрицы Z-, У- и Я-параметров. Связь между одними и теми же величинами, выраженными через различные системы параметров, представлена в табл. 5.1. В этой таблице определители AY, AZ и АН соответствующих матриц определяются выражениями

AY = УцУзз - Y12Y21, AZ = Z11Z22 - 212Z21, АН = Я11Я22 --Я12Я21. (5.11)