Таблица 5.1

Уравнения (5.1), (5.4), (5.7) и аналогичные им другие уравнения позволяют построить эквивалентные схемы замещения четырехполюсников.

На рис. 5.2, а изображена схема замещения, построенная в соответствии с уравнением (5.1). На этой схеме оба напряжения Ej и Ej рассматриваются как напряжения внешних источников. Генератор тока V12E2 учитывает влияние выходного напряжения Е2 на входной ток Ii, а генератор тока Y21E1 - влияние напряжения Ej на выходной ток I2. Оба генератора можно рассматривать как зависимые источники, так как обеспечиваемые ими токи пропорциональны напряжениям внешних источников. Параметр Yi имеет смысл взаимной проводимости от входа к выходу, а У12 - от выхода к входу. Очевидно также, что Уц есть входная проводимость четырехполюсника при Е2 = О, т. е. при коротком замыкании выхода, а У22 - выходная проводимость при возбуждении четырехполюсника от источника Е2 при коротком замыкании входа.

Эквивалентная схема четырехполюсника, соответствующая уравнениям (5.4) и (5.5), изображена на рис. 5.2, б. На этой схеме зависимые источники напряжения Z12I2 и Z21I1 учитывают влияние 1 на Е и li на Ез соответственно. Уравнениям (5.7), (5.8) соответствует схема замещения, показанная на рис. 5.2, в.

Здесь необходимо отметить следующую особенность активного четырехполюсника: как правило, У21 # У12 или 21 Ф Zi2, Я21 ф Hi2- Это означает, что активные четырехполюсники необратимы и, следовательно, принцип взаимности к активным четырехполюсникам неприменим.

Взаимные проводимости или сопротивления пассивных четырехполюсников, как известно, равны (теорема взаимности). Это позволяет схемы замещения, показанные, например, на рис. 5.2, а и б, упростить для пассивного четы-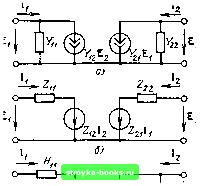

Рис. 5.2. Схемы замещения четырехполюсника, основанные на матрице:

а) У-параметров; б) Z-параметров; в) Я-параметров

Наличие общей шины на рис. 5.2 и в последующих аналогичных схемах позволяет говорить о трехполюснике. Это не влияет иа уравнения цепи.

22 -21.

Рис. 5.3. Преобразование схем замещения, изображенных на рис. 5.2, а и б, справедливое только для пассивного четырехполюсника

рехполюсника и привести их к виду, при котором зависимые источники отсутствуют (рис. 5.3).

При анализе радиоэлектронных цепей особенно часто приходится иметь дело с четырехполюсниками, возбуждаемыми только со стороны входа; под выходным напряжением при этом подразумевается падение напряжения на сопротивлении нагрузки Z„ = l/G,,, тегЕа = - г. В подобных случаях нагрузочный элемент целесообразно вводить внутрь четырехполюсника.

При представлении четырехполюсника с помощью У-матрицы получается схема замещения, показанная на рис. 5.4, а, которая отличается от схемы на рис. 5.2, а только тем, что нагрузочная проводимость G„ введена в четырехполюсник. Это позволяет рассматривать новый четырехполюсник как разомкнутый, у которого ток на выходе I2 = 0. Матрица параметров этого нового четырехполюсника

[У] =

11 12 21 2 2

где Г22 = 122 + (iy,-

Второе уравнение (5.1) принимает при этом вид

12 = 21 El -f• Угг Ез = о,

откуда следует важное соотношение

Ез К21 21

22"

(5.12)

(5.13)

""Т-Ял Ж

г:

•Л

I 12

Рис. 5.4. Введение нагрузочного элемента в состав четырехполюсника

Исключив с помощью этого соотношения Ei из первого уравнения (5.1), а также учитывая, что Е, = - IjZh, получим отношение токов

У2 Он

(5.13)

где АУ = (У22 + G„) - У12У2! - определитель матрицы (5.12).

При использовании Z-матрицы схема замещения принимает вид, показанный на рис. 5.4, б. В данном случае выходные зажимы замкнуты накоротко (Ег = 0), а матрица параметров

2,2 22-2 J

где Z22 = Z22 + Z„.

Второе уравнение (5.4) при этом приводится к соотношению

(5.14)

а первое уравнение - к соотношению

Е2 Z21 Zh Z21 Zh

Z, 1 Z - Z, 2 Zi

12 -21

(5.14)

где AZ = Zii (Z22 + Z„) - Z12Z21 - определитель матрицы (Z).

Наконец, второе уравнение (5.7) при подстановке Яг = -f G„ и Е2 = - l22„ (рис. 5.4, в) дает

0 = 21 Ii-f Яз Е2-=Я21 Ii-Z„ I2,

откуда следует соотношение

Я z„

(Я22-f G„) Z„

Zh Я.2-(- 1

(5.15)

Исключив с помощью этого соотношения Ii из первого уравнения (5.7), получим

El Яц -Я12 Я21

где ДЯ = Яа (Я22 + G„) -Я12 Я21.

(5.15)

>22 2

)ГУ2Г->/2Е/

CZ2/ Z,2)i, I2

О °

Рис. 5.5. Схемы замещения с одним зависимым источником тока (а) или напряжения (б) (элемент Z22 следует заменить на Z22-Z12)