Из сравнения уравнения (5.30) с (5.1) следует, что введенный выше параметр S совпадает с параметром Vji (Для схемы с ОЭ). Подставив в (5.29) 1„ = -G„ Ез и разделив полученное уравнение на Ej, приходим к следующей формуле:

Кя« - S/(Л3.2 ] G„) - h.n /?вх (/2-2 -i

которая отличается от (5.27) лишь внешне.

В тех случаях, когда проводимость /I22 мала по сравнению с проводимостью нагрузки Gj,, можно пользоваться приближенными формулами

К, « h.

21» •

(5.31) (5.32)

Работа транзисторного усилителя по схеме с ОЭ в режиме малого сигнала иллюстрируется рис. 5.8, б. Амплитуда переменного тока коллектора /„ во много раз меньше постоянного тока /ко> соответствующего напряжению смещения (/бэо-

Приведем аналогичный пример для усилителя на электронной лампе.

Схема простейшего усилителя на пентоде изображена на рис. 5.9, а. При малом сигнале (режим линейного усиления) связь между анодным током и напряжениями сетка-катод, анод-катод определяется соотношением

S«c„ + (1 /Ri) "ак = S (Ucb + "ан).

(5.33)

при «(.„-£0. «ак"=-ао;

при «„=£,0, «аь-

D = MSRi - проницаемость по управляющей сетке (соотношение справедливо при работе без сеточного тока).

Крутизна S характеристики/а («ск) и внутреннее сопротивление пентода Ri являются дифференциальными параметрами, определенньши при незначительных отклонениях тока ig от исходного значения Iao в рабочей точке на вольт-амперной характеристике пентода.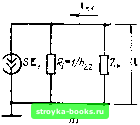

Рис. 5.8. Схема замещения коллекторной цепи (а) и режим линейного усиления колебания в усилителе с ОЭ (б)

1,50

-о о-

Сетка о

-о о-

Катод

о Анод

Е2=-1а2н

су ffJ

Рис. 5.9. Простейший усилитель на пентоде (о) и схема замещения анодной цепи (б)

Знак плюс перед вторым слагаемым в выражении (5.33) выбран в связи с тем, что Ыак в данном случае рассматривается как напряжение независимого источника.

Для тока цепи сетки можно составить выражение, аналогичное (5.33)

(5.34)

В данном случае наиболее удобна система У-параметров.

Переходя к комплексным амплитудам и имея в виду общую схему замещения активного четырехполюсника (рис. Ъ.2,а), заменяем «„к амплитудой El входного гармонического сигнала, ток /<, в цепи сетки - амплитудой 11, а ток /а - амплитудой = 1а- Как и в предыдущем параграфе [см. вывод формулы (5.13)] полагаем Ег = - ан = -вых- Тогда уравнения (5.1) и (5.3) запишутся так:

1. -

~- Е, Sprt Ej, I... - SEi = -- Ej;

"ok

(5.35)

При усилении слабых сигналов рабочая точка на характеристике а («ск)> как правило, устанавливается в области отрицательных напряжений В этом случае ток сетки отсутствует, входная проводимость сетка-катод практически равна нулю (R оо) и матрица проводимостей принимает вид

[Г[-

(5.36)

Таким образом, Кц = К,о О, У = S, Yi = Ь/?;-

Матрице (5.36) соответствует схема замещения четырехполюсника

(трехполюсника), представленная на рис. 5.9, б.

Используя формулу (5.17), находим коэффициент усиления напряжения

SRj Zh

Ri + 2„

/?i + Z„

(5.37)

где ц = SRi - ID - коэффициент усиления лампы.

Из (5.37) видно, что усилительная способность лампы используется тем полнее, чем больше отношение ZJRi. В холостом режиме (Z„ ->- оо) коэффициент усиления каскада

шах Ke--V = -SR, -S/G;.

5.3. ЧАСТОТНЫЕ И ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ РАДИОЭЛЕКТРОННЫХ ЦЕПЕЙ

Приведенные в предыдущем параграфе выражения (5.17), (5.18) для коэффициентов усиления Ке и К/ можно трактовать как передаточные функции линейного активного четырехполюсника. Характер этих функций определяется частотными свойствами параметров Z и К.

Записав Кв и К/ в виде функций Кя (ш). К/ (im), приходим к понятию передаточная функция линейного активного четырехполюсника K(jw). Безразмерная в общем случае комплексная функция К(м) является исчерпывающей характеристикой четырехполюсника в частотной области. Она определяется в стационарном режиме при гармоническом возбуже-нии четырехполюсника.

Передаточную функцию часто удобно представлять в форме

К{ш) =KHef(K (5.38)

Модуль К (w) иногда называют амплитудно-частотной характеристикой (АЧХ) четырехполюсника. Аргумент ф (со) называют фазо-частотной характеристикой (ФЧХ) четырехполюсника.

Другой исчерпывающей характеристикой четырехполюсника является его импульсная характеристика g (t), которая используется для описания цепи во временной области.

Для активных линейных цепей, как и для пассивных, под импульсной характеристикой цепи g (t) подразумевается отклик, реакция цепи на воздействие, имеющее вид единичного импульса (дельта-функции). Связь между g (t) и К(м) нетрудно установить с помощью интеграла Фурье.

Если на входе четырехполюсника действует единичный импульс (дельта-функция) ЭДС со спектральной плотностью, равной единице для всех частот, то спектральная плотность выходного напряжения равна просто К(ш). Отклик на единичный импульс, т. е. импульсная характеристика цепи, легко определяется с помощью обратного преобразования Фурье, примененного к передаточной функции K(iw):

g(t)~ Г K(iM)e«dw. (5.39)

2л J

- оо

При этом необходимо учитывать, что перед правой частью этого равенства имеется множитель 1 с размерностью площади дельта-функции. В частном случае, когда имеется в виду б-импульс напряжения, эта размерность будет [вольт X секунда].

Соответственно функция К(м) является преобразованием Фурье импульсной характеристики:

K{i()==\ g(t)e-"dt. (5.40)

В данном случае перед интегралом имеется в виду множитель единица с размерностью [вольт х секунда]-.

В дальнейшем импульсную характеристику будем обозначать функцией g (t), под которой можно подразумевать не только напряжение, но и любую другую электрическую величину, являющуюся откликом на воздействие в виде дельта-функции.