Как и при представлении сигналов на плоскости комплексной частоты (см. §2.14), в теории цепей широко распространено понятие передаточной функции KipV, рассматриваемой как преобразование Лапласа от функции

g (ty-

KiP) =g{t)e->4p.

(5.41)

Переходная функция цепи h (t) представляет собой отклик, реакцию цепи на воздействие, имеющее вид «единичного скачка». Так как такое воздействие является интегралом от единичного импульса (т. е. дельта-функции), то и между h (t) и g (t) существует интегральное соотношение t

h{t)\g{x)dx. (5.42)

В последующих главах при анализе передачи сигналов через радиоцепи в основном будет применяться импульсная характеристика g (t).

5.4. АПЕРИОДИЧЕСКИЙ УСИЛИТЕЛЬ

Схема замещения простейшего апериодического резистивного усилителя представлена на рис. 5.10. Усилительнш прибор обозначен в виде зависимого источника тока SEi с внутренней проводимостью Gi = l/Ri. Емкость Со включает в себя межэлектродную емкость активного элемента и емкость внешней цепи, шунтирующие нагрузочный резистор R„ = 1/G„. Схема на рис. 5.10 является обобщенной, она применима к любому активному элементу.

. Для транзисторного усилителя под крутизной S следует подразумевать величину /laig/Bx (™. § 5.2), а под С,- - параметр /tog. Подставив в формулу (5.27) проводимость G,- вместо Ягг, а ткже G = 1/н + iaCg = G„ + icdCq, получим передаточную функцию однокаскадного усилителя

Ki (ш) - . J. . = - f. =--."" , (5.43)

l + iwCo/(Gi + Cn)

1 -f («Ti

К\ max = S/(G,+G„)

(5.44)

- максимальный коэффициент усиления (при со = 0); = Co/(Gj + GJ = = RsCo - постоянная времени цепи, состоящей из конденсатора Сд, шунтированного резистором Ra = l/(Gi -f- G).

Pkc. 5.10. Схема замещения резистивного усилителя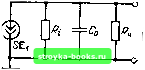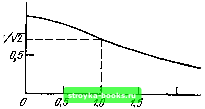

2,0 uiTf

Рис. 5.11. Амплитудно-частотная характеристика апериодического усилителя, представленного на рис. 5.10

* Здесь и в дальнейшем обозначения передаточной функции цепи, рассматриваемой как преобразование Фурье или Лапласа от импульсной характеристики g (t), будут различаться только аргументом К (ш) или К (р) (см. §2.13).

Запишем (5.43) в форме

Ki da)- Ki (со) еч"<«> =--""" еЧ" (5.45)

откуда вытекают следующие выражения для амплитудно- и фазо-частотной характеристик:

Ki(co) - Кх шах/КНЧ. (5.46)

Ф1 (со) == -arctg CDTj. (5.47)

При изменении частоты со получается АЧХ, изображенная на рис. 5.11.

Полоса пропускания усилителя Acoi, определяемая по ослаблению на границах до МУ. от максимального уровня (при со = 0), легко находится из условия

Ki(Ami)- Кшах/Kl + (Ami xf К, шах/КЗ", (5.48)

откуда AcojTi = 1; Awj = I/tj.

5.5. КАСКАДНОЕ СОЕДИНЕНИЕ ИДЕНТИЧНЫХ АПЕРИОДИЧЕСКИХ УСИЛИТЕЛЕЙ

Однокаскадный усилитель позволяет получить относительно небольшое усиление - в десятки или сотни раз. Обычно требуется во много раз большее усиление. Эта задача решается с помощью многокаскадных усилителей, составленных из нескольких, обычно одинаковых, ступеней. Современная микроэлектронная элементная база позволяет почти полностью исключить влияние выходной цепи на входную. Это позволяет считать отдельные каскады «развязанными», благодаря чему результирующая передаточная функция всего усилителя может быть выражена произведением передаточных функций отдельных каскадов, рассматриваемых порознь. Если к тому же все каскады идентичны, то при общем их числе п передаточная функция всего усилителя

К„ (fw) = [Ki (ico)]" = ( - \" - ( -1)" Кп (м) е"Р <>. (5.49)

V l-f(COTi /

Здесь

n(«) = K?„3x/n+(coTi)Y/2 (5.50)

i(u)) = -п arctg wTi (5.51)

представляют собой соответственно АЧХ и ФЧХ всего усилителя.

Из выражения (5.51) видно, что ФЧХ усилителя ф„ = /гф1 совпадает по форме с ФЧХ одного звена фь но ее масштаб по оси ординат возрастает в п раз. Амплитудно-частотная характеристика Кп (<») изменяется по форме: с увеличением п она становится острее.

Рассмотрим более подробно характеристики двухкаскадного усилителя.

При л == 2

КгН- К\шг.1{\+{Ш1)% (5.52)

Полоса пропускания Awj, определяемая, как и ранее, по ослаблению К (ш) на границах до 1/1/2 от максимального значения (при w = 0), должна отвечать условию 1 + (AuijTi) = ]/2, откуда следует равенство

Дша т 154

1 = 1/К2- 1 0,644. (5.53)

Таким образом, полоса пропускания всего усилителя составляет 0,64 от полосы каждого из каскадов (AcoiTi = 1). При п = 3 АЧХ усилителя принимает вид

K3H-K?max/[l+WP/2. (5.54)

Полоса пропускания AcogXi определяется из условия [1 + (AcOgXi)!*/ = = 12, откуда получается равенство

АсозТ1=К2/з 1 я0,51. (5.55)

Нетрудно обобщить полученные результаты на любое значение п:

Дсо„Т1 = К2/« -1 . (5.56)

В табл. 5.2 приведены значения Acd„Ti для различных п. Обычно задается определенная полоса пропускания усилителя в цело.м. Поэтому с увеличением числа каскадов полосу пропускания каждого из них необходимо увеличивать. Например, при заданной полосе двухкаскадного усилителя Acu2 полоса пропускания одного каскада, равная l/xj, должна быть Д0)2/0,644 = 1,55А(02 (см. табл. 5.2). Представляет интерес выявить зависимость формы АЧХ от п при заданной и неизменной полосе пропускания усилителя в целом. С этой целью обратимся к формуле (5.52) и представим знаменатель правой части в виде показательной функции. Основываясь на со-

отношении а

- Ina

записываем

•ln[l-t- ((от,)»]

[l + (cuTiY2=e - - 57)

Обозначив (coTi) = х, представим In (1 + х) в виде степенного ряда*. \п(1+х)=-х + У2хЧ-/,х + ... прихК1. (5.58)

Из табл. 5.2 следует, что при л> 1 в пределах полосы пропускания A(o„Ti величина wxj значительно меньше единицы, а х = (сот,) < 1. Так, уже при п = 3, X < 0,51 х 0,25 и второй член в разложении (5.58), т. е. VjX, не превышает л; 0,03. Можно Поэтому ограничиться лишь первым членом в разложении (5.58): In (1 + х) » х- (wtj).

При этом (5.57) переходит в

•(сот,)

[l+(MTi)]"/2>.

и модуль передаточной функции будет

(5.59)

Итак, с увеличением п (}юрма АЧХ приближается к колоколообразной. Это свойство многокаскадного усилителя, составленного из идентичных, взаимно независимых каскадов, часто используется Для построения фильтров с колоколообразной АЧХ (гауссовских фильтров). Вопрос об усилении сиг-

Т абл ица 5.2