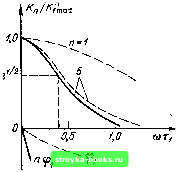нала является при этом второстепенным, основное значение имеет увеличение крутизны скатов АЧХ, а также скорости убывания «хвостов» АЧХ (см. §2.12).

При со = 1/]/лт1 последнее выражение приводит к соотношению

Следовательно, величину Acoq = l/j/nxi можно трактовать как полосу пропускания гауссовского фильтра, определяемую по ослаблению АЧХ до e-V2 = 0,606 от максималь-

Рис. 5.12. Амплитудно- и фазо- ного значен ия /<7 max •

частотная характеристики ше- Если задана полоса фильтра АсОц, то по-

стикаскадного усилителя лоса пропускания одного каскада должна

быть Acoj = 1/ti = Yn Асоц. Определим ФЧХ подобного фильтра. В общем случае ФЧХ определяется формулой (5.53). Учитывая, однако, что cotj <<( 1 [см. рассуждения, приводящие к формуле (5.59)1, можно исходить из упрощенного выражения

Ф„ (со) -ncoTj. (5.60)

Таким образом, окончательно передаточная функция л-каскадного усилителя-фильтра (при л > 1)

Кп{ш)-Кп,..е~"ое-"" (5.61)

[множитель (-1)" опущен].

Амплитудно- и фазо-частотная характеристики шестикаскадного усилителя изображены на рис. 5.12. АЧХ одного каскада, а также шести-каскадного усилителя, вычисленные по точным формулам (5.46) и (5.49), показаны штриховой линией. Последняя получается возведением в шестую степень характеристики одиночного каскада. Характеристика соответствующего гауссовского фильтра, вычисленная по приближенной формуле (5.59), показана сплошной линией.

5.6. РЕЗОНАНСНЫЙ УСИЛИТЕЛЬ

Схема простого резонансного усилителя на транзисторе с ОЭ (рис. 5.13, а) отличается от апериодического усилителя только цепью нагрузки. В данном случае нагрузкой является резистор шунтирующий параллельный колебательный контур L С. Как правило, потерями мощности в катушки индуктивности L и конденсаторе С можно пренебречь по сравнению с мощностью, выделяемой в резисторе R. При этом условии полная проводимость нагрузки (между зажимами 1-2)

G„ = G+icuC+l/icuL.

Приведем основные параметры контура LC с шунтом резонансная частота сОр = \IYLC;

характеристическое сопротивление р = YiLlC = cOpL = l/cOpC;

затухание а„ = \I2RC;

постоянная времени Тк = 2RC = 1/а„;

добротность Q - -5а- = = -5iPliL = .

р 1/шрС 2

-о о-

-ко aj

ИВых (Ф)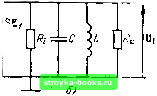

Рис. 5.13. Резонансный усилитель (а) и схема замещения коллекторной цепи (б)

Исходя ИЗ схемы замещения усилителя (рис. 5.13, б) и основываясь на формуле (5.27) (с заменой /ijj на G,), определяем передаточную функцию усилителя

Ке(1С0)= -

Gj + Gui-fKoC-f l/icoZ.

(G,•-fGш) .

(5.62)

Слагаемое (G, + Gu,)/C = 1 ?э„С = 2аэк в знаменателе выражения (5.62) учитывает шунтирующее влияние активного элемента на затухание контура.

С учетом приведенных выше обозначений параметров контура передаточная функция (5.62) приводится к виду

(5.63) (5.64)

Для высокодобротных контуров основным параметром является значение передаточной функции усилителя на частотах, близких к резонансной частоте сОр. В этом случае выражение (5.63) можно привести к виду

К(1сй)

С 2аэ

1 , . 2((0-(Ор) I--l(C0 -Шр)Тэ„

+ Van

,(5.65)

где Ктах = Si{Gi 4- Gm) - максимальное усиление (на частоте сй.= сОр); Тэь- - постоянная времени контура с учетом влияния внутренней проводимости активного элемента G,-. Величину

«3H-Q«K-(C0-C0p)t,, Шр

часто называют обобщенной расстройкой Итак, выражение (5.65) можно записать в форме

К (ICD) =

= (а,,) е--

(5.66) контура.

(5.65) 157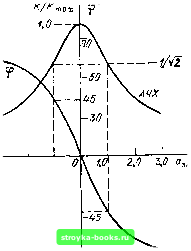

-г,о -zfi -1,0

Характеристики К («ак) и Ч («эн) резонансного усилителя представлены на рис. 5.14.

Относительная полоса пропускания резонансного усилителя, определяемая по ослаблению амплитуды на границах полосы до 1 \2 от .максимального уровня (при 0) и выраженная через обобщенную расстройку а,,, равна 2 (см. рис. 5.14). Для перехода от безразмерной относительной полосы пропускания 2 к размерной полосе 2Асй„ .положим в (5.66) Кк = 1, а Да) Д(!)(,. Тогда

где Qa, как это следует из (5.66), добротность нагруженного контура.

В заключение приведем упрощенное выражение для импульсной характеристики резонансного усилителя

g(0 «(-S/C) еcos СОр?. (5.65

Рис. 5.14. Амплитудно- и фазо-частотная характеристики одноконтурного резонансного усилителя

Сопоставление выражений (5.65) и (5.43) указывает на то, что передаточную функцию резонансного усилителя можно получить посредством сдвига передаточной функции соответствующего апериодического усилителя на оси частот на величину Шр. Следует лишь постоянную времени Xj = = Co/(G; 4 G) приравнять величине Тэ.

Все сказанное можно распространить также и на каскадное соединение идентичных резонансных усилителей. Приведенная с{юрмула (5.61) позволяет сразу написать аналогичное выражение для передаточной функции резонансного /г-каскадного усилителя (фильтра)

К,1 (до) К"\ max е

..р)2/2Д规 -

(5.68)

где Aoj„„ 1/ лта,; ~ Дсо„ 1л, а Асоо када.

полуширина полосы одного кас-

5.7. ОБРАТНАЯ СВЯЗЬ В АКТИВНОМ ЧЕТЫРЕХПОЛЮСНИКЕ

При анализе линейных усилителей в § 5.2-5.6 на базе .матриц параметров эквивалентных четырехполюсников основное внимание уделялось параметрам Y., Z, Hi, поскольку именно эти параметры определяют усилительную способность активного четырехполюсника. В реальных, не полностью однонаправленных активных четырехполюсниках приходится считаться с воздействием выходного колебания на вход усилителя.

Пусть в рабочем режиме усилителя напряжение и ток на выходе будут Ег и Ij. Рассматривая эти величины как результат внешнего воздействия со стороны выхода, можно определить If и Ег на входе с помощью схемы заме-щения~(рпс. 5.15). На этой схеме зажимы /-/, к которым подключен входной источник сигнала, условно замкнуты накоротко, а под напряжением, действующим на зажимах 2-2, гюдразумевается Е{ -= -Z/ IJ, т. е. паде-