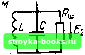Рис. 5.23. К примеру определения устойчивости усилителя с обратной связью

нения (5.84) должны быть либо отрицательными действительными величинами либо комплексными величинами с отрицательны.ми действительными частями. Из этих простых физических представлений вытекает следующий фундаментальный критерий устойчивости любых линейных систем*: система устойчива, если действительные части всех корней характеристического уравнения отрицательны. Заметим, что левая часть характеристи-представляет собой не что иное, как знамена-

ческого уравнения (5.84) тель передаточной функции цепи, записанной в форме

bop" + bl p"~-t.. -tbm-1 P + brn

(5.85)

Таким образом, корни характерист.ического уравнения цепи являются полюсами передаточной функции К{р} этой цепи.

Отсюда следует, что сформулированные выше условия отрицательности действительных частей корней равносильны следующему положению: для устойчивости цепи необходимо, чтобы передаточная функция К.{р) не имела полюсов в правой полуплоскости комплексной переменной р.

Это хорошо известное из теории цепей положение можно распространить и на передаточную функцию Ко (р) цепи с обратной связью. Поясним это на примере резонансного усилителя с обратной связью (рис. 5.23).

Передаточную функцию (по напряжению) усилителя определим по формуле (5.70):

Ку (Р)

С р2 + 2аэ

;Р + «

а передаточную функцию цепи обратной связи Кос (р) приравняем ±M/L, где М - взаимная индуктивность.

Тогда передаточная функция усилителя, охваченного обратной связью.

Ко(р) =

Ку (Р)

1+Ку(р)Кос С р2-Ь(2аэ„-ЬКос5/С)рИ-

Находим корни уравнения р -Ь (2а,дк -f Кос SIC) р -Ь шр = О

Кос

Pi, 2 - ""эк -

Крс 2С

Рассмотрим два возможных случая: отрицательной и положительной обратной связи.

Для создания отрицательной обратной связи произведение КуКос должно быть отрицательной величиной. Поскольку Ку (ш) при со = Шр, т. е. при резонансе, является отрицательной величиной, то коэффициент Кос должен быть положительной величиной: Кос - -\-M.lL. При этом действительные части обоих корней pi и Рг

Re (Pi,2) = -(a3„+MS/2LC)

отрицательны при любом значении М.

При положительной обратной связи

Re (Pi,2)=-

Кос = -M/L; <0приЛ15/21С<аэк> >0приЛ!5/21С>аэк-

(5.86)

Это фундаментальное положение было обосновано А. М. Ляпуновым, который в 90-х годах прошлого века заложил основы теории устойчивости. Рассматриваемый вопрос об устойчивости состояния покоя системы является частным случаем общей теории устойчивости Ляпунова.

Итак, при отрицательной обратной связи рассматриваемая цепь устойчива при любом значении М, а при положительной обратной связи - только при выполнении условия

Кос1 =

М 2Саэк

утах

где ЛГутах ~ SRm = 5/0ш - коэффициент усиления на резонансной частоте [см. (5.65)1.

В тех случаях, когда цепь описывается дифференциальным уравнением высокого порядка, исследование корней характеристического уравнения, необходимое для решения вопроса об устойчивости системы, является сложной задачей.

Оказывается, что ее можно решить, анализируя соотношения между коэффициентами уравнения без определения самих корней уравнения. Это можно выполнить с помощью теоремы Гурвица, которая утверждает, что для того, чтобы действительные части всех корней уравнения

с действительными коэффициентами и fe„ > О были отрицательными, необходимо и достаточно, чтобы были положительными все определители Aj, А2, А, составленные из коэффициентов уравнения Ь„, Ь, fe„ по следующей схеме;

Ьз &5

Ai = fci, А2 =

А4 =

bl b, bo b.

5 b,

2 14

0 bl bs fcs 2 bi

0 bo b

bo b, 0 bl &з

3 5 7 bo

&2 bl bg bg

bl bs fc- b

bo &2 4 bg

0 0 bibs b,

и т. д.

Сформулированный алгебраический критерий устойчивости часто называют критерием Рауса - Гурвица. При составлении определителей по указанной схеме коэффициенты с индексом, превышающим степень характеристического уравнения, заменяются нулями.

Поэтому, например, для уравнения четвертой степени получаются следующие определители:

Ai = bi, Д2

bl bs bo bi

A3 =

bl bs bo bi 0 bl

bl bs bo b

2 &4 0

0 bl bs 0

0 bo &2 bl

Нетрудно видеть, что все последовательные определители являются главными диагональными минорами о*пределителя "АТак как последний столбец определителя А содержит лишь один отличный от нуля элемент Ьт, расположенный на главной диагонали, то выполняется равенство

Ат=, Am-l-

1 Доказательство этой теоремы см., например, в книге: Курош А. Г. Курс высшей алгебры. - М.: ГИФМЛ, 1972.

Отсюда следует, что в соответствии с теоремой Гурвица условия устойчивости можно формулировать в виде следующих неравенств:

Ai>0, А2>0,..., Л„ , >0, fc„,>0.

Так, для характеристического уравнения второй степени Ai = &1 > О, &2 > О, (5.87)

для уравнения третьей степени Ai = &1 > О,

А2 =

Ьо 2

bib-bboX), &з>0, (5.88)

т. е. bi > О, bi&2 > bgbg, bg> 0. Так как 6, bi и Ьз положительны, то и

Й2> 0.

Для уравнения четвертой степени:

1. Ai = fei>0, 2. As-feifca -&3&o>0.

3. Ag = 63(6162-63 )-&?&4> О, 4. 64 >0.

Из условия 3 на основании условий 4 и 1 вытекает неравенство

63(61 б2-6„6з)>б!б4>0.

Поэтому условие 3 можно заменить условием 63 > 0. Таким образом, для уравнения четвертой степени получаются следующие условия устойчивости:

>0, 63 > О, 63 (бЛ - 6„6з) - 6? 64 > О, 64 >0. (5.89)

Поясним применение критерия Гауса-Гурвица на простом примере рассмотренного резонансного усилителя с обратной связью (см. рис. 5.23). Характеристическое уравнение этой цепи при Кос " (отрицательная обратная связь)

Сформулированные для уравнения второй степени условия устойчивости (5.87) в данном случае принимают вид

Ai = 6i = 2a« + -->0. 6.,=со>0.

Первое условие выполняется при любом значении М > О, а второе от М не зависит.

При положительной обратной связи (Кос = -MIL) цепь устойчива при выполнении условия 2а„-(M/L) (5/С) > О, совпадающего с (5.86).

Критерий Рауса-Гурвица особенно удобен для проверки устойчивости цепи с заданными параметрами (т. е. коэффициентами дифференциального уравнения). Однако им неудобно пользоваться при экспериментах, так как обычно бывают известны не коэффициенты уравнения, а передаточная функ-ния разомкнутой цепи К.у{р) Кос (Р)- Кроме того, критерий Рауса-Гурвица не дает ясных указаний, как неустойчивую цепь сделать устойчивой.