5.10. ЧАСТОТНЫЕ КРИТЕРИИ УСТОЙЧИВОСТИ

(5.90)

Требование, чтобы передаточная функция Ко(р) = Ку(р)/[1-Ку(Р)Коо(р)]

не имела полюсов в правой полуплоскости р = а -\- ia, т. е. в области, ограниченной полуокружностью бесконечно большого радиуса R и осью iw (рис. 5.24, а), равносильно условию, что знаменатель выражения (5.90), не должен иметь нулей в указанной oблacти или, что то же самое, функция

Н(р) = Ку(р)Кос(Р) (5.91)

не должна обращаться в единицу ни в одной из точек правой полуплоскости р. Но Н{р) представляет собой передаточную функцию разомкнутого кольца обратной связи, т. е. отношение напряжения на зажимах 2-2 к напряжению на зажимах /-/ при разомкнутом кольце, как это показано на рис. 5.25. Следовательно, об устойчивости системы с обратной связью можно судить по характеристикам разомкнутого тракта.

Для дальнейшего анализа целесообразно перейти от плоскости р - а-\-ш к плоскости Н{р) =u-\-iv (рис. 5.24, б). Каждой точке р плоскости 0, ICO соответствует определенное значение Н на плоскости и, iv. Любой замкнутый контур на плоскости р преобразуется с помощью выражения (5.91) в некоторый (также замкнутый) контур на плоскости Н.

Если исходный контур на плоскости р задан в виде контура на рис. 5.24, а, соответствующий ему контур на плоскости Н называется годографом функции Н.

Показанный на рис. 5.24, а контур С можно разбить на два участка: 1) прямая ш от оо до - оо и 2) полуокружность бесконечно большого радиуса R.

На первом участке, где 0=0, р - ш, функция Н(р) обращается в функцию Н(/о)). В соответствии с выражением (5.91) этот участок преобразуется на плоскости Н в линию, определяемую следующим соотношением:

Н (ш) = Ку (ш) Кос (М = («) ос («) е Су+ос) = „ (О)) 4- iv (О)), (5.92) откуда и(й))

у («)Л:ос,(«)С05 (фу + фос),

v («) = Ку (ffl) /Соо {) sin (фу + Фос).

(5.93)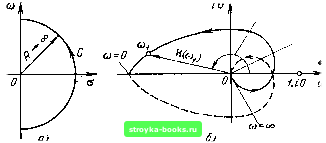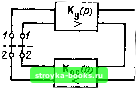

Рис. 5.25. К определению передаточной функции разомкнутого тракта

Рис. 5.24. Замкнутый контур иа р-плоскости (а) и годо- усилитель - четырехпо-граф функции Н (ш) на плоскости u+iv (б)

люсник обратной связи

Предполагается, что основной усилитель устойчив, т. е. Ку (р) не имеет полюсов в правой полуплоскости р.

в этих выражениях фу и фо - аргументы передаточных функций соответственно четырехполюсников Ky(tco) и Koc(tw).

На втором участке контура С (см. рис. 5.24, а) при R -4- оо функция Н (р) 0. Это вытекает из общего выражения

К{р)В (Р-Ро.)(Р-Ро.)... (Р-Ро.) „ (Р-Рш) (Р -Рлз)--- (Р-пт)

которое При \р\ ->оо можно представить в виде Bp"-" (здесь В-постоянный коэффициент, а /?о; и pnt - соответственно нули и полюсы функции К (р))-

Совершенно аналогично и функцию Н (р) при \р\-оо можно представить в форме Н (р) = где п и m - числа соответственно нулей и полюсов функции Н (р).

При л< m и \р\ -оо модуль функции Н (р) на полуокружности R -> ->-оо равен нулю*. Таким образом, полуокружность бесконечно большого радиуса R на плоскости р преобразуется в точку, лежащую в начале координат на плоскости Н, и для построения годографа Н в виде замкнутого контура достаточно знать поведение Н (р) на оси гш, т. е. знать АЧХ и ФЧХ цепи Ку (ш) Кос («)•

Обходу контура С на рис. 5.24, а в положительном направлении (против часовой стрелки) соответствует обход годографа Н при изменении частоты от оо до -оо, т. е. также против часовой стрелки (см. рис. 5.24, б).

Очевидно, что вся правая полуплоскость р преобразуется на плоскости Н во внутреннюю область годографа. Следовательно, если годограф передаточной функции разомкнутого тракта не охватывает точку 1, Ю, то при замкнутой цепи обратной связи система устойчива, в противном случае система неустойчива.

Это условие называется критерием устойчивости Най-к в и с т а.

Показанная на шк;. 5.24, б диаграмма соответствует устойчивой системе. Это видно из тогочто годограф Н не охватывает точку 1, Ю. Сплошной линией показана часть контура, соответствующая положительным частотам О <; ы <; о°, а штриховой - часть контура, соответствующая отрицательным частотам. Так как функция и (со) четная, а v (со) нечетная относительно О), то оба участка годографа симметричны относительно действительной оси.

Следует также отметить, что рис. 5.24, б построен для случая, когда при со = О передаточная функция Н (гсо) отлична от нуля (это возможно, например, для усилителей постоянного тока, в которых отсутствуют разделительные конденсаторы).

При сложной схеме цепи форма годографа иногда бывает настолько усложненной, что по ней трудно судить о том, охватывается или не охватывается годограс}юм точка 1, /0. В подобных случаях оказывается полезным критерий, вытекающий из критерия Найквиста, основанный на подсчете числа пересечений оси и (о) на участке 1, ор. Для устойчивости цепи необходимо, чтобы годограф либо вообще не пересекал этот отрезок (как на рис. 5.24, б), либо пересекал его в положительном и отрицательном направлениях одинаковое число раз.

Критерий Найквиста получил наибольшее распространение в радиоэлектронике, автоматике и других смежных областях. Основное его преимуще-

Имеются в виду наиболее распространенные в практике четырехполюсники с пе" редаточной функцией у которой степень числителя п меньше степени знаменателя т-

ство: удобство оперирования АЧХ и ФХ разомкнутой цепи. В некоторых системах, например содержащих линии, этот метод по существу является единственно приемлемым.

Суть частотного критерия можно наглядно пояснить не прибегая к полярным диаграммам, на основе обычных АЧХ и ФЧХ разомкнутой цепи КуКос-

Действительно, длина вектора Н (ш), как это ясно из выражения (5.92), есть не что иное, как модуль коэффициента передачи разомкнутой цепи КуКос т. е. АЧХ этой цепи, а аргумент ф„ (рис. 5.26), равный

фя = arctg -- Фу (О)) 4- фое («), U (ш)

(5.94)

есть ФЧХ цепи КуКос-

Совместив на общем графике АЧХ и ФЧХ, нетрудно ответить на вопрос об устойчивости цепи.

Если при изменении оо от О до оо фаза фн не достигает 2я, то замкнутая цепь устойчива при любом значении КуКос - С другой стороны, если К-уКос при любой частоте меньше единицы, то цепь устойчива при любой ФЧХ. Цепь неустойчива если имеются частоты, при которых одновременно выполняются два условия:

Фу-f Фо(. = «2я, tt -целое число, Я == Лу/Сое 1 •

(5.95)

По существу эти два условия необходимы для обращения в нуль знаменателя в выражении (5.76), определяющем передаточную функцию замкнутой цепи.

Пример АЧХ и ФЧХ устойчивой цепи с обратной связью показан на рис. 5.26, а неустойчивой - на рис. 5.27. В первом случае на частоте со,,, соответствующей фу -f Фос = 2я, модуль Я <: 1. Во втором случае oOj, - частота паразитной генерации. На рис. 5.26 и 5.27 отложены абсолютные значения фу -f фос. При учете знака реальных фу и фос наклон ФЧХ будет отрицательным.

При построении этих характеристик учтено, что при оо = О и со = оо величина /Су/Сое обращается в нуль. При оо -> О это обусловлено влиянием последовательно включенных конденсаторов в канале Ку или Кос при 00 оо - влиянием шунтирующих емкостей (межэлектродных, монтажа и т. д.). Полное изменение фазы при изменении оо от О до оо зависит от числа звеньев в усилителе и в цепи обратной связи.

Для более сложных цепей, когда набег фазы в тракте КуКос может быть больше 2л, приходится прибегать к критерию Найквиста.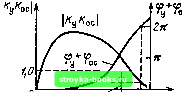

Рис. 5.26. Амплитудио- и фазо-частотная характеристики устойчивого усилителя с обратной связью

Рис. 5.27. Амплитудно- и фазо-частотная характеристики неустойчивого усилителя