Для реальных цепей всегда выполняется условие

g{t - х) О при t< X, (6.10)

т. е. при отрицательном аргументе функция g (t - х) должна обращаться в нуль, так как отклик не может опережать воздействие. Поэтому выражение (6.8) можно заменить выражением

5вых(0= j S{X)g(t-x)dx (6.11)

- 00

(при ЭТОМ имеется в виду, что для х> t подынтегральное выражение обращается в нуль).

Приведем, наконец, еще одну форму записи, которая получается из выражения (6.8) при замене л: на t - и:

s,,,At)=-\s{t~-x)g{x)dx =5 s(«)g(-«)rf«. (6.12)

Интеграл, стоящий в правой части выражения (6.8), в математике называется сверткой функций s (t) и g (t) (см. § 2.7). Таким образом, приходим к следующему важному положению: сигнал Sj,b,x (О выходе линейной цепи является сверткой входного сигнала s (t) с импульсной характеристикой цепи g (t).

Из выражения (6.8) видно, что сигнал на выходе цепи sx (О в момент t получается суммированием мгновенных значений входного сигнала s (t), взятых с весом g (t - х) за все предыдущее время.

В § 6.2 при суммировании спектра входного сигнала весовой функцией являлась передаточная функция цепи К (ш)- В данном случае при суммировании мгновенных значений входного сигнала s (t) весовой функцией является импульсная характеристика цепи, взятая с аргументом (t - х), т. е. функция g (t - х).

Из рис. 6.2, б, построенного для момента времени t> т, видно, что отклик цепи на воздействие s (х) не может закончиться раньше, чем функция g (t- х) сместится вправо от s (х) на время, равное длительности импульсной характеристики т,. Иными словами, сигнал на выходе цепи не может быть короче Xg + tg.

Для того чтобы при прохождении через цепь сигнал не удлинялся, требуется выполнение условия О, т. е. импульсная характеристика цепи должна приближаться к дельта-функции, а это равносильно требованию равномерности передаточной функции К (/со) при О -< со <. оо.

В § 6.4, 6.5 рассматривается прохождение некоторых управляющих сигналов через апериодические цепи. Все остальное содержание главы посвящено анализу передачи радиосигналов через узкополосные цепи.

6.4. ПРОХОЖДЕНИЕ ДИСКРЕТНЫХ СИГНАЛОВ ЧЕРЕЗ АПЕРИОДИЧЕСКИЙ УСИЛИТЕЛЬ

Диск ретные сигналы обычно представляют собой последовательности импульсов. При передаче таких последовательностей через инерционные цепи срма импульсов претерпевает изменения, что приводит к частичной или полной потере передаваемой информации. В связи с этим одной из наиболее типичных задач является анализ искажения формы импульсов.

Из всего многообразия импульсов наибольший интерес для анализа представляет прямоугольный импульс. Это обусловлено простотой его

формирования, а также широким применением в системах с двоичным кодом и во многих других радиотехнических устройствах. При этом основное внимание обычно уделяется передаче фронта и среза импульса. Этот вопрос особенно важен, когда передаваемая или извлекаемая информация содержится в положении переднего (или заднего) перепада импульсов на оси времени (например, в некоторых радиолокационных системах).

Рассмотрим прохождение прямоугольного импульса через однокаскадный резистивный усилитель, изученный в § 5.4 и дополненный на выходе разделительной цепью RpC (рис. 6.3, а). Назначение этой цепи - защита транзистора от постоянного напряжения, имеющегося в устройстве формирования входного сигнала.

При гармоническом возбуждении на частоте со и амплитуде входной ЭДС E-i напряжение на входе транзистора (в предположении, что /?р значительно меньше входного сопротивления база-эмиттер)

Ui =

Rp-\- 1/icoCp

=Е,Кр(И,

(6.13)

где Кр (гм) = twTp/(l + imp) - передаточная функция разделительной цепи; Тр = /?рСр - постоянная времени этой цепи.

Схема замещения коллекторной цепи усилителя представлена на рис. 6.3, б. От схемы на рис. 5.10, а она отличается тем, что напряжение Ej заменено напряжением Uj = Ei Кр (го)).

Передаточная функция Ki (t«) однокаскадного резистивного усилителя определяется с}юрмулой (5.43), а рассматриваемого устройства в целом - выражением

-i =Kp(iO))Ki(/o))- Р *"«

К(гсо)==Нвых. = Н£Н2 Е, Ui

l+!fOTp l+icoT,

где Tl = RCq.

График /((w), вычисленный по с}юрмуле

K(w) = K,,

(ОТт

T/l+((0Tp)2 Vl + (C0T,)2

при Tp/xi = 100 представлен на рис. 6.4.

В операторной форме передаточная функция:

К (Р) = -Кивах,, -

--{Л+рТр)(1 f pTi)

Пусть в момент = О на вход усилителя подается прямоугольный импульс ЭДС е (t) с амплитудой Е и длительностью Т (рис. 6.5, а). В интервале времени от = О до = Т напряжение на выходе усилителя можно рассматривать как результат включения при t - О постоянной ЭДС е, (t) = Е.

Рис. 6.3. Транзисторный усилитель с разделительной /?С-и,епью на входе (а) и схема замещения выходной цепн (б)

0 0,1 0, 0,6 0,8 1,0 1,2 ыг.

Рис. 6.4. Амплитудно-частотная характеристика усилителя, представленного на рис. 6.3, а

В момент t -- Т включается дополнительная ЭДС е.2 (t) -=- -Е, компенсирующая первую (рис. 6.5, б). Суперпозиция выходных напряжений щ (t) и и.2 (t), обусловленных действием (t) и (t), образует импульс на выходе усилителя. Таким образом, задачу можно свести к рассмотрению переходного процесса в усилителе при включении на входе постоянной ЭДС.

Изображение по Лапласу для ei (t)= Е, t > О, в соответствии с (2.102) будет

Ё(р)={ e,(f)e-pdpE-p.

Тогда по формуле (6.3) выходное напряжение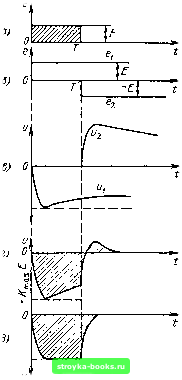

w,(0 =

- ЕК ip) е" dp =

С + too С-IOC

(1+рТр) (1 lpT,)

Рис. 6.5. Искажение формы импульса в резистивном усилителе:

а) импульс на входе; б) представление импульса в виде суммы двух скачков;

в) деформация скачков на выходе;

г) результирующий импульс на выходе; д) импульс на выходе усилителя при устранении разделительной пепи

Полюсы подынтегральной функции:

р,= -1/Тр, р., = -~1/т„ Т, <Тр. Вычислив вычеты по формуле (6.6), приходим к следующему результату:

«,(0- я(е--е-/.). (6.14)

Графики «1 (t) и щ (t) = -«1 (t - Т) изображены на рис. 6.5, в, а результирующее напряжение на выходе усилителя и (t) = и, (t) (t) - на рис. 6.5, г.

Из формулы (6.14) и рис. 6.5, г видно, что при малых временах, т. е. при t, соизмеримых с Tj, первая экспонента в выражении (6.14) близка к единице и основное влияние на фронт импульса оказывает вторая экспонента. Когда же / становится соизмеримым с Тр, характер функции (t) определяется в основном первой экспонентой. То же самое относится к функции (t) при отсчете времени с момента t = Т. Прямоугольный импульс с амплитудой Ктах, который имсл бы мссто В идсальном усилителе без разделительной цепи изображен на рис. 6.5, г штриховой линией.

Искажение формы реального импульса проявляется: а) в конечной крутизне фронта и среза, б) в спаде вергиины импульса