
 |
|
Главная Цепи и сигналы [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [ 59 ] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] [167] [168] [169] Первый из этих факторов выражен тем сильнее, чем больше постоянная времени Tl = RC (и, следовательно, чем сильнее завал частотной характеристики в области верхних частот). Второй фактор (спад вершины импульса), наоборот, выражен тем сильнее, чем меньше постоянная времени Тр разделительной цепи RCp (и, следовательно, чем сильнее завал частотной характеристики в области нижних частот). Выбор постоянных времени Xi и Хр зависит от требований, предъявляемых к форме импульса на выходе усилителя. Если требуется, чтобы за время Т амплитуда лишь достигала своего максимально возможного значения КтахЕ, то постоянная врСмеНи Tj может быть близка к Т. Форма импульса при этом далека от прямоугольной. В тех случаях, когда требуется удовлетворительное воспроизведение формы импульса, постоянная времени Xi должна сопоставляться со временем, отводимым на длительность фронта выходного импульса, а постоянная времени Тр должна быть велика по сравнению с длительностью импульса Т. Этот результат имеет важное значение для правильного выбора параметров системы передачи дискретных сигналов, так как он указывает минимальное время, необходимое для перехода от одного дискретного уровня к другому. Следует отметить, что в случае усиления импульсной последовательности проведенное выше рассмотрение справедливо при достаточно длительном интервале между импульсами, так что наложение переходных процессов от соседних импульсов не имеет места. Рассмотрим теперь прохождение прямоугольного импульса через один транзисторный апериодический усилитель (схема на рис. 5.10), без разделительной цепи. Для этого достаточно устремить емкость Ср к бесконечности, т. е. закоротить конденсатор Ср. При этом формула (6.14) переходит в "i(0=-Kn,ax£(l-e-/-), (6.14) так как Хр с». Импульс на выходе.рассматриваемого усилителя изображен на рис. 6.5, д. 6.5. ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ СИГНАЛОВ В радиоэлектронике часто требуется осуществлять преобразование сигнала, имеющее характер дифференцирования или интегрирования. На вход линейного устройства, осуществляющего дифференцирование, подается сигнал s {t); с выхода должен сниматься сигнал вида ds(i) вых if) - Xfj- В интегрирующем устройстве связь между выходным хых (О и входным S {t) сигналами должна иметь следующий вид: .ь,х(0 = - fs(/). То J в этих выражениях Tq - постоянная величина, имеющая размерность времени. Дифференцирование и интегрирование являются линейными математическими операциями. Следовательно, для дифференциального или интегрального преобразования сигнала следует применять линейные цепи и элементы, обладающие требуемыми соотношениями между входными и выходными ве- О-1 °--° Рис. 6.6. Простейшая цепь, используемая Рис. 6.7, Дифференцирующая цепь для дифференцирования или интегрирования личинами. Этим требованиям отвечают в принципе такие элементы, как обычные конденсаторы или катушки индуктивности в сочетании с резистором при надлежащем съеме выходного сигнала. Рассмотрим сначала цепь, изображенную на рис. 6.6. Подразумевая под входным сигналом s (t) ЭДС, составляем уравнение для тока в цепи i (t) Riit) +-iit)dis(l). (6.15) Умножив это уравнение на С и обозна чив постоянную времени цепи т = RC, получим V (О + .[ i(0 d/- Cs (О- (6.16) Характер функциональной связи между током i (t) и входны.м снгнало.м s (t) зависит от постоянной времени т. Рассмотрим два крайних случая: очень малого и очень большого Хд. При очень малом Tq первым слагаемым в левой части уравнения (6.16) можно пренебречь. Продифференцировав оставшееся после отбрасывания этого слагаемого уравнение по t, получим Отсюда видно, что напряжение на резисторе R, совпадающее по форме с i(t), пропорционально производной входного сигнала г.. п/- ds (О ds (О ur = Ri {t)MRC- o-jT dt dt Таким образом, приходим к схеме дифференцирующего четырехполюсника, показанной на рис. 6.7, в которой выходной сигнал сни.мается с резистора R. При очень больших значениях То второе слагаемое в левой части уравнения (6.16) можно отбросить. При этом ток т,, R совпадает по форме с входным сигналом, а напряжение на конденсаторе С, равное s{t) dt, пропорционально интегралу от входного сигнала s (t). Отсюда следуег, что для осуществления интегрирования RC-цепь должна быть такой, как пока зано на рис. 6.8. Аналогичные результаты можно получить с помощью RL-цепи (рис. 6.9 и 6.10). Постоянная времени Тд = L/R дифференцирующей цепи должна быть достаточно мала, а интегрирующей - достаточно велика. Прг; !пдиф(})е- ренцирования для первой схемы (см. рис. 6.9) можно представить следующим образом. При достаточно большом сопротивлении R ток через /?£-цепь почти не зависит от L и совпадает по форме с входным сигналом s (t). Выходной же сигнал Sgix (0. снимаемый с индуктивности L, dt dt -I МО ds (t) в схеме, показанной на рис. 6.10, наоборот, ток в основном определяется индуктивностью L (так как R весьма мало): i{t)j-s{t)dt, выходной же сигнал, снимаемый с резистора R, s,u{i)=Ri{t)-{s{t)dt. То J Уточним теперь использованные выше понятия «малое» и «большое» Tq. Это проще всего сделать на основе спектрального рассмотрения. Если входной сигнал S (t) имеет спектральную плотность S (w), то при точном дифференцировании выходной сигнал *выхи/ - То -- dt должен иметь спектральную плотность што5 (со), а при точном интегрировании - плотность (1/шТо) S (со) fcM. (2.59) и (2.60)]. Это означает, что для точного дис})ференцирования требуется четырехполюсник с коэ()фициентом передачи К (гсо) = То/со, (6.17) а для точного интегрирования К (tco) = 1/тогсо. (6.18) Передаточные функции показанных на рис. 6.7 и 6.8 четырехполюсников соответственно К(/со) =-2-= RC----= " , (6.19) R+l/iaC 1+Ш(0 l-fTo(o) К (ico)=-i/i =-!--i-= --1-. (6.20) Из сравнения выражений (6.17) и (6.19) видно, что для удовлетворительного ди(}х)еренцирования требуется, чтобы выполнялось условие тосо«1. (6.21) Это неравенство должно удовлетворяться для всех частот спектра входного сигнала, в том числе и для самой высокой. 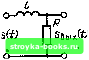 Рис. 6.8. Интегрирующая Рис. 6.9. Дифференци- Рис. 6.10. Интегрирую-цепь рующая цепь щая цепь [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [ 59 ] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] [167] [168] [169] 0.0016 |