Рассмотрим механизм формирования собственного шума в резистивном и резонансном усилителях.

В резистивном усилителе сопротивление Z„ (ш) определим для схемы на рис. 5.10, а по формулам

l/icoCo

l + (o)Co Rf

(7.15)

Постоянная времени цепи RCq во много раз больше длительности импульса Tg-, соответственно полоса пропускания цепи RCg, примыкающая к нулевой частоте, во много раз уже, чем ширина спектра Wi (со), показанного на рис. 7.2. Поэтому при определении воздействия на цепь дробового шума его можно рассматривать как белый шум со спектром Wi (со) = el о-Тогда по формуле (7.14)

\17„(со)-=г/о R-l[\+{<Co Rf] и по сюрмуле (4.39)

R{r)eIoR- j

i + (u)Co R}

cos (OX

(7.16)

dco.

Входящий в правую часть\[нтеграл

cos (ОТ

{i/RCof + fo

dco - - RCexp

Таким образом,

RCo I

(7.17)

При t = 0 это выражение определяет дисперсию напряжения шума о1 и среднеквадратическое напряжение шума ст:

(7.18)

Нормированная корреляционная функция шума

.г„(т)-=ехр(-]т1/ВД. (7.19)

Графики спектра W (со) и функции r„ (т) изображены на рис. 7.4 и 7.5.

Интервал корреляции напряжения шума в данном примере определяется величиной \x\IRCq I. Нетрудно пояснить смысл полученного результа-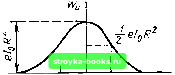

-f,o о 1,0

-1,0

Рис. 7.4. Спектр шумового напряжения на выходе резистивного усилителя

Рис. 7.5. Нормированная корреляционная функция шума, соответствующая спектру tfuCco) (рис. 7.4)

та. Напряжение шума на нагрузке образуется совокупностью беспорядочно следующих импульсов тока, создаваемых отдельными электронами. Каждый из этих импульсов создает импульс напряжения, длительность которого определяется постоянной времени нагрузки. При наложении большого числа импульсов относительная скорость изменения суммарного напряжения шума и (t) должна быть того же порядка, что и скорость изменения отдельных импульсов. Поэтому для независимости напряжений, отсчитываемых в моменты / и ; + т, величина т должна быть не менее длительности импульсов, образующих шум.

Для количественной оценки напряжения шума, создаваемого дробовым эффектом, приведем следующий пример, характерный для апериодического усилителя: постоянный ток /ц = 10 мА, сопротивление нагрузки R = 5 кОм, емкость Со = 50 пФ.

Применяя формулу (7.18), находим среднеквадратическое напряжение шума на выходе усилителя

"-"""-»-1=2,8.0-Б = 0,28мВ.

2.50.10-12

Определенное таким образом напряжение можно условно рассматривать как результат приложения некоторого напряжения шума ко входу усилителя. При коэффициенте усиления Ку эквивалентное напряжение шума на входе следует приравнять величине и = oJKy. При коэффициенте усиления Ку « 100 получаем Wg„ « 3 мкВ. Это значение и определяет нижний порог сигнала, который еще имеет смысл усиливать данным усилителем.

Аналогичным образом можно рассмотреть формирование шума в колебательной цепи резонансного усилителя, схема которого изображена на рис. 5.13.

По аналогии с выражением (7.14) определим спектр W,{(iy)-=Wi (со) ZIk (со) = е/о ZIk (со), (7.20)

(Ш) = -12 «-5ш- ,

+«зк . , . 2(м-о)р)

1 + (-сэк

а р - Rm - сопротивление контура (шунтированного резистором /?ш) при резонансе. Отсюда квадрат модуля сопротивления нагрузки

Zk(o3) = /?/(l-f(a)-cOp)42], (7.21)

где т„ = 2(2эк/сОр - постоянная времени контура. Таким образом,

(со) =е/о/?/(1 +(ш-сОр)Н]. (7.22)

График спектра W„ (ы) изображен на рис. 7.6.

Выражение (4.39) для корреляционной функции в данном случае принимает следующий вид:

- оо о

Рис. 7.6. Спектр шумового напряжения на выходе резонансного усилителя

2гт/й}р

I гк

Рис. 7.7. Нормированная корреляционная функция, соответствующая" спектру WuM (рис. 7.6)

Переходя к новой переменной coi = со - сор, получаем eh

fCOS (0,1 , . f sin(o,T , ---асо, - 51пы т I---асо.

cos СОр т

Заметим, что при достаточно большой добротности контура выполняется условие

c0pT, = c0p(2Q3,/c0p) = 2Q3,» 1.

Поэтому нижний предел интегралов -Ыр можно заменить на -оо. Второй интеграл обращается при этом в нуль вследствие нечетности подынтегральной функции относительно переменной интегрирования со. Первый же интеграл вследствие четности подынтегральной функции приводится к виду

с COS (О, т

cos Ml т

Аналогичный интеграл был вычислен при выводе формулы (7.17). Используя этот результат, получаем

(,) !h3k cos СОр т е-1/к =

xl 2

= е-"« cos CO. т = е/о R а„ е"" cos Шр т.

(7.23)

Здесь через а„ = 1/тк обозначено затухание контура. Учитывая, что при шунтировании контура сопротивлением коэффициент затухания а„ = = 1/2/?щС записываем сюрмулу (7.23) в следующей форме:

/?u(T) = -e-«HNcoscppT.

(7.23)

Из сюрмул (7.23), (7.23) вытекает, во-первых, что средний квадрат напряжения шума на контуре

al=.R(Q)=eIoRlyOL=eIoRj2C (7.24)