и среднеквадратическое напряжение шума ст„ = Ve/o/?„,/2C; во-вторых, нормированная корреляционная функция определяется выражением

г„(т) -е~"«" coscOpT = e~"«coscOpT. (7.25)

График функции г„ (т) показан на рис. 7.7. Интервал корреляции в рассматриваемом случае определяется ходом огибающей функции г„ (т), т. е. множителем е~™к в выражении (7.25).

Пересчет напряжения шумов ко входу усилителя, как и для апериодического усилителя, можно сделать по формуле ик = JKy, в которой под Ку следует подразумевать коэффициент усиления на резонансной частоте.

Напряжение шума, выделяемое на высокодобротном колебательном контуре, показано на рис. 4.17. Приведенные в § 4.6 характеристики узкополосного случайного процесса могут быть полностью отнесены к дробовому шуму в резонансном усилителе.

Нужно иметь в виду, что изложенный в данном параграфе материал дает представление лишь о методе анализа характеристик собственных шумов, формируемых избирательной цепью усилителя. Механизм образования шумов зависит от ряда физических и конструктивных особенностей усилительных (активных) элементов, которые здесь не рассматриваются.

В заключение укажем, что приведенные выше соотношения можно использовать также при анализе теплового шума в избирательных цепях. Необходимо лишь спектр такого шума определять по формуле, известной из физики,

W„ (со) = 2kTR, (7.26)

где -сопротивление резистора, генерирующего шум; fe = 1,38 X X 10-" Вт - с/град - постоянная Больцмана; Г - асболютная температура.

Тепловой шум является белым шумом.

Как и в выражении (7.12), (со) здесь определено для положительных и отрицательных частот. При отнесении мощности шума только к положительным частотам коэффициент 2 следует заменить на 4.

7.4. ДИФФЕРЕНЦИРОВАНИЕ СЛУЧАЙНОЙ ФУНКЦИИ

Пусть задан стационарный эргодический случайный процесс s (t) со спектром Ws (со) и корреляционной функцией Rs (т); требуется найти аналогичные характеристики для производной s (t). Не останавливаясь здесь на рассмотрении всех условий дифференцируемости случайной функции, ограничимся основным требованием: энергетический спектр Ws (со) при ы оо должен убывать быстрее, чем 1/со, так что

co2W,(co)cico<c5o. (7.27)

- сю

Это условие выполняется для большинства практических задач, так как спектр Ws (со) формируется физической цепью, передаточная функция которой при ы оо убывает быстрее, чем 1/со (а квадрат модуля уменьшается быстрее, чем 1/со). Условию (7.27) не отвечает белый шум с бесконечно широким спектром, однако обычно рассматривается шум с ограниченным спектром.

Считая условие (7.27) выполненным, рассмотрим прохождение случайного сигнала s (i) через идеальную дфференцирующую цепь, передаточная функция которой К (tco) = IcoTo [см. (6.17)1.

Применяя выражения (7.2), (7.3), можем написать

вых и = К (ш) (ш) = т со Ws (ш), (7.28)

.выхМ=-Го- j" шГДсо)е»Мш. (7.29)

- оо

Дисперсия процесса на выходе устройства ?..вь,х=вык= j fflr,(co)do3. (7.30)

WsH--

Рассмотрим следующий пример. Пусть спектр процесса на входе дифференцирующего устройства равномерен в полосе частот -/i/A

Wo при ] ш 1 2k/i = Acuj, О при ю1 >2nfi =Ami. Корреляционная функция подобного процесса [см. (4.41)1 i?,(T) = ro2i(sinAffliT/AffliT),

а дисперсия

Ds=al = Rs{0)Wo2h. (7.31)

Нормированная корреляционная функция

Га (т) = (sin Aa)iT)/AcOiT. (7.32)

После дифференцирования получаем йвыхМ TotoWo и

R,Buxb)=<Wo - f cos (отЛо = i" -ij(2 AcoiT cos Аш,т + я J я X

+ [(AffliT) -21 sin Ашт}.

Домножив числитель и знаменатель на (Awi) и учитывая, что

Го Ao)i= Го2л/1=яа„

приводим предыдущее выражение к виду

«вых(т) =(A(OiTo)al «/(AffliT), (7.33)

где у (A(Oi т) = (А©! т) ~ {2AmiT cos Acoi т + [(Acoj т)- 2] sin Ao)i т}.

При т -> О получается неопределенность вида О/О. Применив правило Лопиталя, получим г/(0) = 1/3. Тогда

ввых(0) = Овых-(Аш1То)(т (/(0)=aTUAcoi)V3. (7.33)

Сопоставляя (7.33) с выражением (4.83), в котором Ашо следует

заменить на Acoj, а Го(т) на гх), приходим к окончательному результату

sBMx(O)- -alxlrliO). (7.34)

В § 7.6 будет показано, что выражение (7.33) справедливо для производной любого стационарного случайного процесса (при К (tu))== t штд).

графики функций Wg (m) и (со), а также функций (т) и

г, вых i) изображены на рис. 7.8, а и б; параметр AwjTo = 1. Из рисунка видно, что дис{)ференцирование приводит к ослаблению нижних частот исходного процесса. Относительное возрастание высших частот приводит к более четко выраженной осцилляции корреляционной функции (см. рис. 7.8, б).

Рассмотрим теперь прохождение того же случайного сигнала через реальное дифференцирующее устройство в виде /?С-цепи (см. рис. 6.7). Квадрат передаточной функции дифференцирующей цепи в соответствии с (6.19)

Таким образом, энергетический спектр на выходе цепи

WM (ДС01Т0)2(С0/ДС0.)

sBHxV / ii 1+(Дсо1Т„)2(со/Дсо,)2 >

график W, вых (*) ДЛЯ A«iTo = 1 представлен на рис. 7.8, а штриховой линией.

Корреляционная функция

авых(т)=Т J

со" COS сот 1 + coHg

d(0,

:(0)-

xlW,

- f -П J 1

+ cotg

dm =

Результат (т) = Rs

[Acoj To-arctg(AmiTo)].

(7.36)

вычисления (T)/a,

нией (для AcojTq = 1).

нормированной корреляционной функции вых представлен на рис. 7.8, б штриховой ли-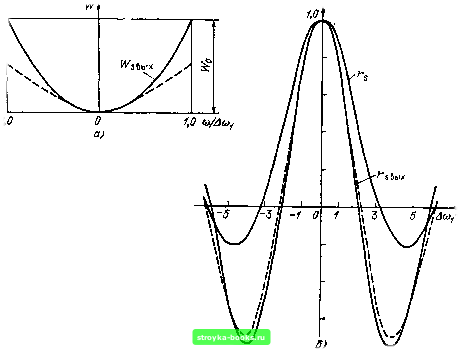

Рис. 7.8. Спектры (а) и нормированные корреляционные функции (б) на входе.и выходе дифференцирующей цепи:

--- на выходе идеальной цепи;

---на выходе ЛС-цепи