
 |
|
Главная Цепи и сигналы [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [ 71 ] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] [167] [168] [169] первые две моментные функции случайного процесса у (t) dx (t)/dt, т. е. процесса на выходе дифференцирующего устройства. Математическое ожидание процесса у (t) М ly{t)]=M ldx/dt]== М lim -i+O-i) Операции осреднения и перехода к пределу перестановочны, поэтому можно написать Mly{t)] drrixi (t) At-*0 M [x(t4-At)]-M[x(t)] At Следовательно, при дифференцировании случайной функции ее момент-ная функция первого порядка также подвергается дифференцированию. Очевидно, что для стационарного случайного процесса первая моментная функция производной равна нулю. Повторяя аналогичные рассуждения для моментной функции второго порядка процесса у (t), можно получить [при условии стационарности процесса X (t)] dx (tl) dx (tj) dt. dmx2 (T) dx d Kx (T) где т = - При т = О M\y(t)] -ajr;(0). (7.50) (7.50 К этому результату, совпадающему с (7.34), можно прийти более простым способом на основе спектральной плотности мощности процесса х (i) и передаточной функции цепи К (im)=to) (для момента второго порядка). Для более сложных цепей, осуществляющих различные линейные преобразования случайного процесса, широко распространен способ,, основанный на стохастических дифференциальных уравнениях, и некоторые другие методы [14[. Приведем теперь пример задачи, когда использование характеристических функций оказывается весьма эффективным способом. Пусть требуется найти плотность вероятности суммы некоторого числа взаимно независимых слагаемых х, Х2, хы. Характеристическая функция суммы имеет следующий вид: = 9..1(л)в,2(г1) ... в,(г1). (7.52) т. е. характеристическая функция суммы независимых случайных величин равна произведению характеристических функций слагаемых. Для частного случая, когда все слагаемые имеют одинаковые распределения и, следовательно, одинаковые характеристические функции в(т1) = 1в,(г1)1 (7.53) Используем выражения (7.45), (7.46) для определения пл(;тности вероятности суммы нескольких гармонических колебаний со случайными фазами. Амплитуды колебаний одинаковы и равны AqI/N. Основываясь на плотности вероятности гармонического колебания (4.25), находим характеристическую функцию ei(il)= - я (7.54) Подставляя е = costja: + is\nr\x и учитывая, что sinTix/Vl - х является нечетной функцией х, получаем (см. 3.753.2 в [28]) i Й1 (Г1) - Г dx = Л (г)), (7.55) где Jo - бесселева функция первого рода нулевого порядка. Для отсчета, взятого из суммы Л гармонических колебаний с одинаковыми амплитудами 1/N, но со случайными взаимно независимыми фазами, характеристическая функция в соответствии с (7.53) будет (7.56) Амплитуда каждой из синусоид приравнена 1/У для того, чтобы дисперсия суммы, равная 0,5N (НУму, оставалась при увеличении числа синусоид неизменной. На рис. 7.9 изображены характеристические функции для различных значений Л. При > 4 функция Qn (ц) быстро приближается к предельной кривой Л/ -> оо, соответствующей нормальному распределению суммы. Для отыскания плотности вероятности суммы N гармонических колебаний необходимо в соответствии с выражением (7.46) вычислить интеграл ры{х) = av(Tl)e-VdTi = - cos r]xdr\. (7.57) При N = 1 получается исходное выражение р (х) для одной синусоиды [формула (4.25)], а при Л/ = 3, 4 функции pn (х) имеют вид, показанный на рис. 7.10. Сплошной линией изображена функция р {х) при нормальном распределении {N оо). Рис. 7.9. Характеристические gZ функции для суммы М гармонических колебаний со случайными фазами -4"
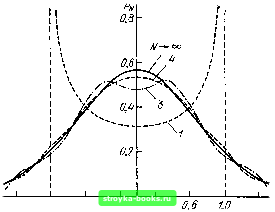 Рис. 7.10. Плотность вероятности суммы Л гармонических колебаний со случайными фазами (рис. 7.1!) -1,0 -0,6 -0,2. О 0,1 1,и X Полученные результаты показывают, что при суммировании хотя бы пятн-шести гармонических колебаний со случайны.ми и взаимно независимыми фазами получается стационарный случайный процесс, близкий к гауссовскому . Это справедливо для значений л:<; YN (при = 1). При больших значениях \х\ ры {х) = 0, в то время как при нормальном распределении р (х) отлично от нуля. Таким образом, при конечном числе слагаемых на «хвостах» кривой распределения неизбежно расхождение между р (х) и 7.7. НОРМАЛИЗАЦИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ В УЗКОПОЛОСНЫХ ЛИНЕЙНЫХ ЦЕПЯХ Пусть на входе линейной цепи (с постоянными параметрами) действует стационарный случайный процесс с распределением, отличным от нормального. Если интервал корреляции этого процесса меньше постоянной времени цепи (т. е. ширина энергетического спектра больше полосы пропускания цепи), то распределение случайного процесса на выходе приближается к нормальному. Эффект нормализации проявляется тем сильнее, чем уже полоса пропускания цепи. Поясним это положение на двух примерах. Сначала рассмотрим воздействие на высокодобротный колебательный контур последовательности коротких, неперекрывающихся, случайным образом расположенных на оси времени импульсов (рис. 7.11), причем постоянная времени контура т„ велика по сравнению со средней величиной интервалов между импульсами. Напряжение на контуре в какой-либо момент времени ti является суммой свободных колебаний, вызванных предыдущими импульсами и не успевших полностью затухнуть к рассматриваемому моменту. Чем уже полоса пропускания цепи, тем длительнее свободные колебания и, следовательно, тем большее число соизмеримых по величине и некоррелированных слагаемых принимает участие в образовании результирующего напряжения в момент t. В соответствии с центральной предельной теоремой эти предпосылки достаточны для приближения распределения к нормальному. При спектральном подходе эффект нормализации можно объяснить следующим образом. Спектр колебания в контуре суммируется из спектров отдельных импульсов входной последовательности. Внутри каждого из этих парциальных спектров фазы спектральных составляющих полностью кор- [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [ 71 ] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] [167] [168] [169] 0.0014 |